Guía de índices y transformación de variables
Índice
Librerías
pacman::p_load(dplyr, summarytools, sjPlot,texreg, corrplot,ggplot2,ggfortify,sandwich,lmtest,sjlabelled)Datos
El Estudio Longitudinal Social del Chile (ENACOES 2014), único en Chile y América Latina, consiste en encuestar a casi 3.000 chilenos, anualmente, a lo largo de una década. ELSOC ha sido diseñado para evaluar la manera cómo piensan, sienten y se comportan los chilenos en torno a un conjunto de temas referidos al conflicto y la cohesión social en Chile. La población objetivo son hombres y mujeres entre 15 y 75 años de edad con un alcance nacional, donde se obtuvo una muestra final de 3748 casos en el año 2018.
load("content/assignment/data/elsoc18p11.RData")#Cargamos la base de datos desde internet
load(url("https://multivariada.netlify.com/assignment/data/elsoc18p11.RData"))Explorar datos
A partir de la siguiente tabla se obtienen estadísticos descriptivos que luego serán relevantes para realizar las transformaciones y análisis posteriores.
view(dfSummary(elsoc, headings = FALSE, method = "render"))| No | Variable | Label | Stats / Values | Freqs (% of Valid) | Graph | Valid | Missing | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | sexo [numeric] | Sexo entrevistado | Min : 0 Mean : 0.6 Max : 1 |
|
3748 (100.0%) | 0 (0.0%) | |||||||||||||||||||||||||||||||
| 2 | edad [numeric] | Edad entrevistado | Mean (sd) : 47.1 (15.5) min < med < max: 18 < 47 < 90 IQR (CV) : 25 (0.3) | 70 distinct values | 3748 (100.0%) | 0 (0.0%) | |||||||||||||||||||||||||||||||
| 3 | educ [factor] | Nivel educacional | 1. 1 2. 2 3. 3 4. 4 5. 5 |
|
3743 (99.9%) | 5 (0.1%) | |||||||||||||||||||||||||||||||
| 4 | pospol [factor] | Autoubicacion escala izquierda-derecha | 1. 1 2. 2 3. 3 4. 4 |
|
3664 (97.8%) | 84 (2.2%) | |||||||||||||||||||||||||||||||
| 5 | part01 [numeric] | Frecuencia: Firma carta o peticion apoyando causa | Mean (sd) : 1.5 (0.9) min < med < max: 1 < 1 < 5 IQR (CV) : 1 (0.6) |
|
3742 (99.8%) | 6 (0.2%) | |||||||||||||||||||||||||||||||
| 6 | part02 [numeric] | Frecuencia: Asiste a marcha o manifestacion pacifica | Mean (sd) : 1.2 (0.6) min < med < max: 1 < 1 < 5 IQR (CV) : 0 (0.5) |
|
3745 (99.9%) | 3 (0.1%) | |||||||||||||||||||||||||||||||
| 7 | part03 [numeric] | Frecuencia: Participa en huelga | Mean (sd) : 1.2 (0.5) min < med < max: 1 < 1 < 5 IQR (CV) : 0 (0.5) |
|
3745 (99.9%) | 3 (0.1%) | |||||||||||||||||||||||||||||||
| 8 | part04 [numeric] | Frecuencia: Usa redes sociales para opinar en temas publicos | Mean (sd) : 1.6 (1.1) min < med < max: 1 < 1 < 5 IQR (CV) : 1 (0.7) |
|
3743 (99.9%) | 5 (0.1%) | |||||||||||||||||||||||||||||||
| 9 | inghogar [numeric] | Ingreso total del hogar | Mean (sd) : 678842.5 (781003.9) min < med < max: 30000 < 5e+05 < 1.7e+07 IQR (CV) : 5e+05 (1.2) | 227 distinct values | 3080 (82.2%) | 668 (17.8%) | |||||||||||||||||||||||||||||||
| 10 | inghogar_t [numeric] | Ingreso total del hogar (en tramos) | Mean (sd) : 7 (5.4) min < med < max: 1 < 5 < 20 IQR (CV) : 7 (0.8) | 20 distinct values | 477 (12.7%) | 3271 (87.3%) | |||||||||||||||||||||||||||||||
| 11 | tamhogar [numeric] | Habitantes del hogar | Mean (sd) : 3.2 (1.6) min < med < max: 1 < 3 < 14 IQR (CV) : 2 (0.5) | 13 distinct values | 3741 (99.8%) | 7 (0.2%) |
Generated by summarytools 0.9.9 (R version 4.0.3)
2021-06-29
view_df(elsoc,max.len = 50)| ID | Name | Label | Values | Value Labels |
|---|---|---|---|---|
| 1 | sexo | Sexo entrevistado |
0 1 |
Hombre Mujer |
| 2 | edad | Edad entrevistado | range: 18-90 | |
| 3 | educ | Nivel educacional |
1 2 3 4 5 |
Primaria incompleta menos Primaria y secundaria baja Secundaria alta Terciaria ciclo corto Terciaria y Postgrado |
| 4 | pospol | Autoubicacion escala izquierda-derecha |
1 2 3 4 |
Derecha Centro Izquierda Indep./Ninguno |
| 5 | part01 | Frecuencia: Firma carta o peticion apoyando causa |
1 2 3 4 5 |
Nunca Casi nunca A veces Frecuentemente Muy frecuentemente |
| 6 | part02 |
Frecuencia: Asiste a mbackground-color:#eeeeeeha o manifestacion pacifica |
1 2 3 4 5 |
Nunca Casi nunca A veces Frecuentemente Muy frecuentemente |
| 7 | part03 | Frecuencia: Participa en huelga |
1 2 3 4 5 |
Nunca Casi nunca A veces Frecuentemente Muy frecuentemente |
| 8 | part04 |
Frecuencia: Usa redes sociales para opinar en temas publicos |
1 2 3 4 5 |
Nunca Casi nunca A veces Frecuentemente Muy frecuentemente |
| 9 | inghogar | Ingreso total del hogar | range: 30000-17000000 | |
| 10 | inghogar_t | Ingreso total del hogar (en tramos) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Menos de |
| 11 | tamhogar | Habitantes del hogar | range: 1-14 | |
Medición y transformación de variables
Creación de índices
En ELSOC existen cuatro preguntas referentes a la participación política o ciudadana, donde se le pregunta a las personas por la frecuencia en que han participado de determinados eventos vinculados a su rol como ciudadanos. Para esto, se emplearon escalas likert de 5 categorías para medir dicha participación.
plot_stackfrq(elsoc[,c("part01","part02","part03","part04")]) + theme(legend.position="bottom")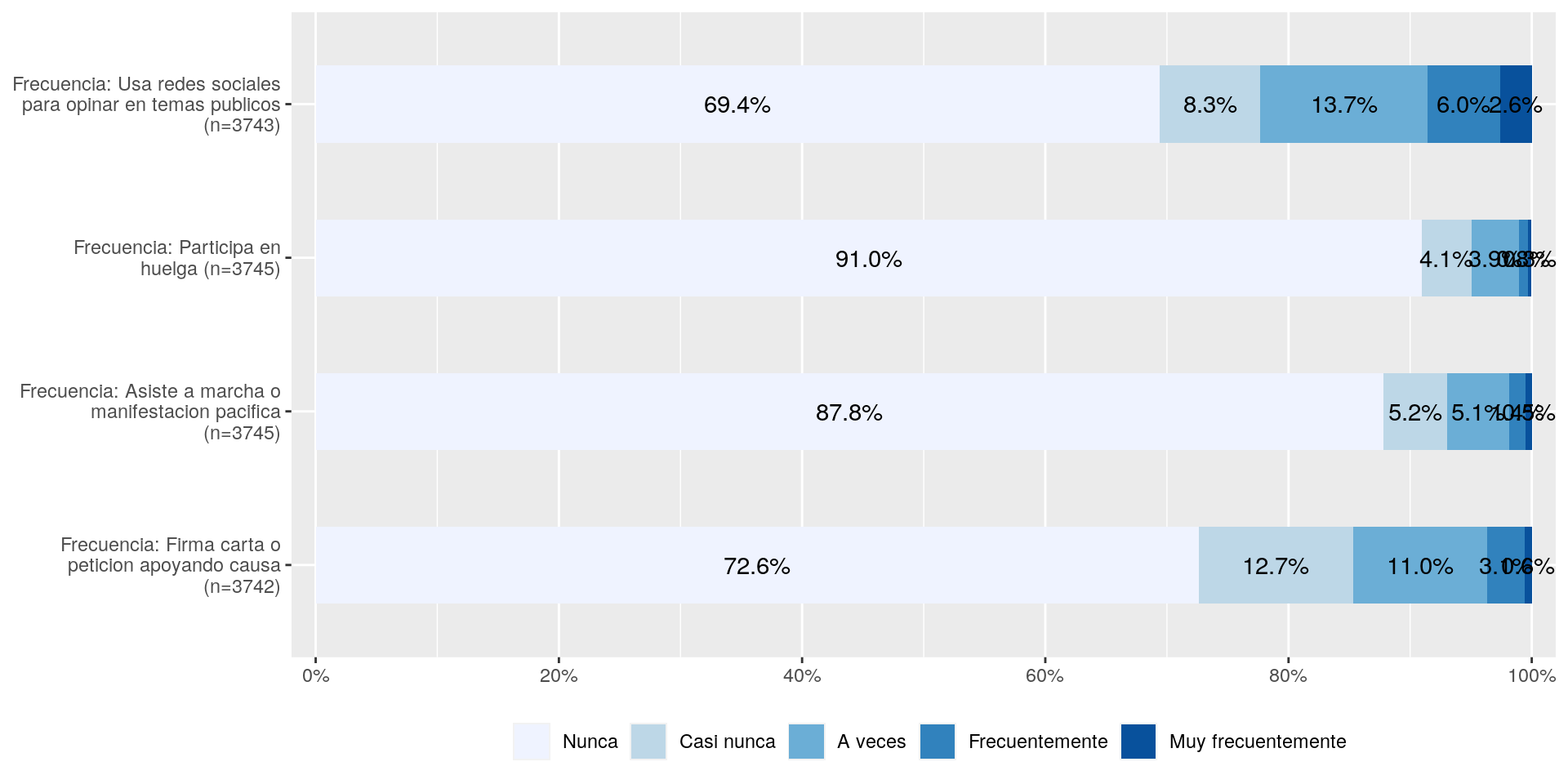
En la figura anterior, podemos ver que existe un alto porcentaje de personas que declaran no haber participado nunca en alguna de estas expresiones de la participación ciudadana. En este sentido, para la creación de un índice o medida agrupada, nos interesa saber si existe algún grado de relación entre nuestros indicadores. Para esto, lo que tradicionalmente se realiza es realizar un análisis de correlación entre los indicadores.
corrplot.mixed(cor(select(elsoc,part01,part02,part03,part04),
use = "complete.obs"))
La matriz de correlación nos indica que existen correlaciones moderadas entre los indicadores, donde 0.25 es la más baja y 0.44 la más alta. Es muy importante realizar este paso, debido a que si nuestros indicadores no correlacionan en absoluto, es posible que estemos frente a un atributo distinto. Por lo tanto, sería poco adecuado realizar la construcción de un índice que busque representar un fenómeno o constructo “común” a través de indicadores que no poseen ningún grado de correlación.
En nuestro caso, hemos decidido elaborar un índice sumatorio a través de la suma de las respuestas de cada individuo. Para ello emplearemos las funciones mutate (para crear una nueva variable) y rowwise() (para sumar los valores de varias filas) de la librería dplyr.
elsoc <- elsoc %>% rowwise() %>% mutate(partpol = sum(part01,part02,part03,part04, na.rm = T))Esta sintaxis genera un índice sumativo en la variable partpol. En caso de índice promedio, simplemente remplazar sum por mean
descr(elsoc$partpol,style = "rmarkdown",stats = "common", transpose = T,headings = F)| Mean | Std.Dev | Min | Median | Max | N.Valid | Pct.Valid | |
|---|---|---|---|---|---|---|---|
| partpol | 5.47 | 2.30 | 0.00 | 4.00 | 20.00 | 3748.00 | 100.00 |
plot_frq(data = elsoc$partpol,type = "hist",show.mean = T)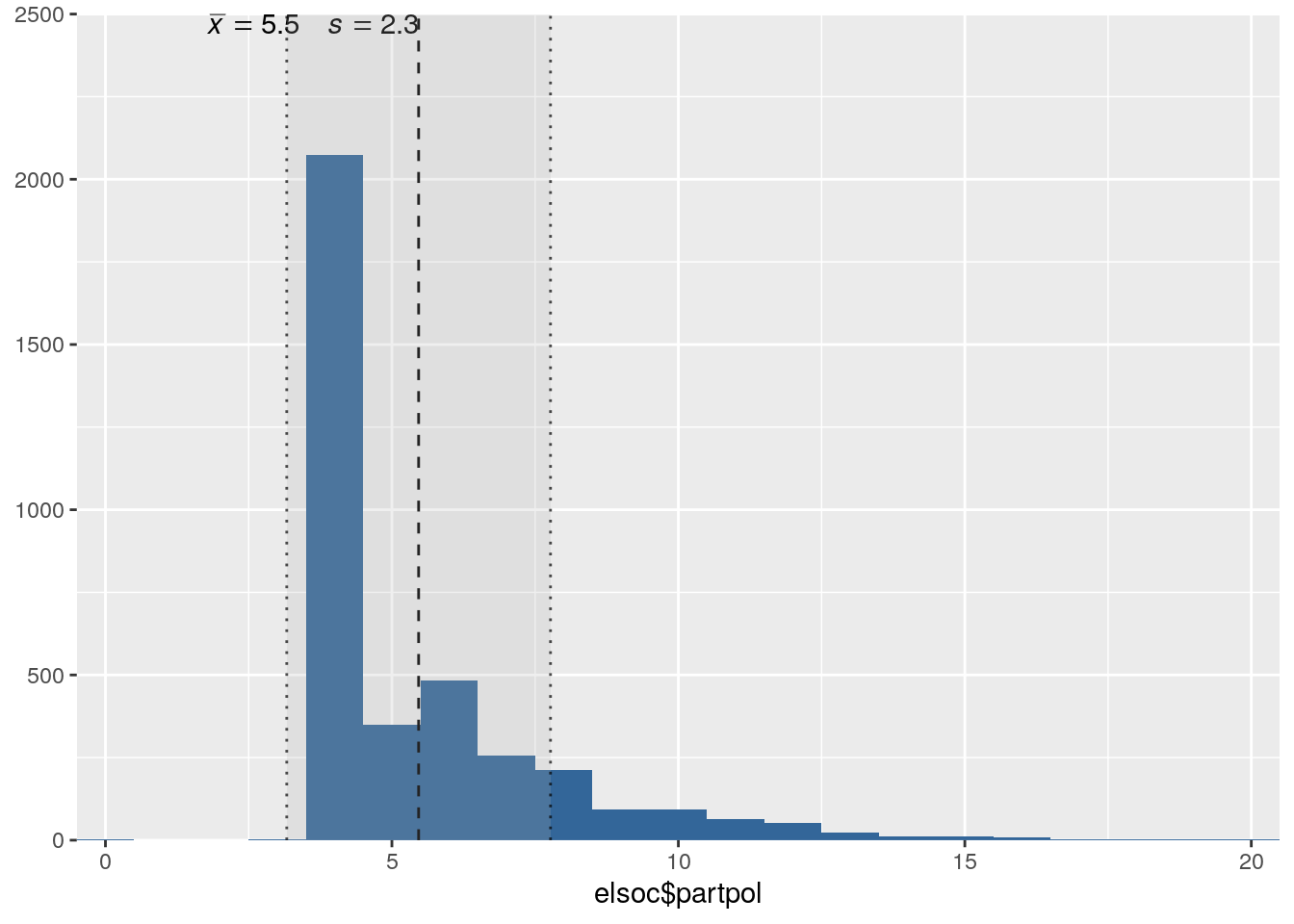
Vemos que el índice sumatorio posee valores que van desde 4 hasta 20, con una media de 5,47 y una mediana de 4. Además, vemos algo que ya se había identificado en el gráfico descriptivo de cada indicador por separado, el hecho que existe una proporción importante de personas que respondieron “nunca” en los cuatro indicadores, los cuales son representados por una alta frecuencia de 4 en el histograma. Con esto hemos creado nuestro índice sumatorio de Participación Política.
Sobre tratamiento de casos perdidos en el índice
Partamos viendo lo siguiente
elsoc %>% select(part01,part02,part03,part04,partpol) %>% filter(is.na(part04))## # A tibble: 5 x 5
## # Rowwise:
## part01 part02 part03 part04 partpol
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 NA NA NA NA 0
## 2 3 3 1 NA 7
## 3 NA NA NA NA 0
## 4 1 1 1 NA 3
## 5 NA NA NA NA 0Acá se muestra una selección de filtrados con NAs en una de las variables (part04), y la información de las variables que componen el índice y la variable partpol, que es el índice sumativo que generamos. Vemos que en el caso que todos los valores de las variables sean NA se genera el valor 0, de otra manera se suma la información disponible. Ante esto se abren una serie de alternativas:
dejar así el valor 0, considerando que puede distorsionar nuestros resultados
reemplazar el valor 0 en esta variable por NA
elsoc$partpol <- car::recode(elsoc$partpol, "0=NA")
# Resultado
elsoc %>% select(part01,part02,part03,part04,partpol) %>% filter(is.na(part04))## # A tibble: 5 x 5
## # Rowwise:
## part01 part02 part03 part04 partpol
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 NA NA NA NA NA
## 2 3 3 1 NA 7
## 3 NA NA NA NA NA
## 4 1 1 1 NA 3
## 5 NA NA NA NA NA- no sumar si es que hay algún caso perdido en la fila (no muy recomendable, ya que se generan muchos casos perdidos). Para esto, simplemente omitir el
na.rm = Tde la sintaxis de generación original
elsoc <- elsoc %>% rowwise() %>% mutate(partpol = sum(part01,part02,part03,part04))
elsoc %>% select(part01,part02,part03,part04,partpol) %>% filter(is.na(part04))## # A tibble: 5 x 5
## # Rowwise:
## part01 part02 part03 part04 partpol
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 NA NA NA NA NA
## 2 3 3 1 NA NA
## 3 NA NA NA NA NA
## 4 1 1 1 NA NA
## 5 NA NA NA NA NARecuperar casos perdidos: ejemplo variable INGRESOS
Es común que en las encuestas sociales cierta variables posean una alta proporción de datos perdidos. Un ejemplo común es en el reporte de los ingresos de los hogares o individuos. Esto generalmente puede generarse por características de la persona (p.ej. desempleado, estudiante) o por deseabilidad social (personas de altos ingresos desisten de reportar). En el caso de ELSOC, existen dos estrategias para solicitar que las personas reporten sus ingresos. La primera consiste en preguntar directamente por el monto en pesos chilenos de los ingresos totales del hogar. Alternativamente, si la persona no reporta los ingresos, se le presenta la posibilidad de ubicar los ingresos del hogar en tramos (Por ejemplo “De
descr(elsoc$inghogar,style = "rmarkdown",stats = "common", transpose = T,headings = F)| Mean | Std.Dev | Min | Median | Max | N.Valid | Pct.Valid | |
|---|---|---|---|---|---|---|---|
| inghogar | 678842.52 | 781003.92 | 30000.00 | 500000.00 | 17000000.00 | 3080.00 | 82.18 |
sjmisc::frq(elsoc$inghogar_t,
out = "txt",
show.na = T) %>% knitr::kable()
|
Si observamos la tabla de descriptivos para la variable ingreso del hogar (inghogar), tenemos un porcentaje 17,82% de datos perdidos. Por esta razón, emplearemos los datos disponibles en inghogar_t para recuperar información en los ingresos del hogar.
La estrategia posee los siguientes pasos:
- Calcular la media del tramo reportado.
- En el caso de que la persona no haya reportado el monto de los ingresos del hogar, remplazamos este valor perdido por el valor de la media del tramo, en el caso de estar disponible.
- Comparamos la variable original con la nueva variable que posee información recuperada.
Paso 1: Calcular la media por cada tramo
elsoc$inghogar_t[elsoc$inghogar_t==1] <-( 220000 ) # [1] "Menos de $220.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==2] <-(220001 +280000 )/2 # [2] "De $220.001 a $280.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==3] <-(280001 +330000 )/2 # [3] "De $280.001 a $330.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==4] <-(330001 +380000 )/2 # [4] "De $330.001 a $380.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==5] <-(380001 +420000 )/2 # [5] "De $380.001 a $420.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==6] <-(420001 +470000 )/2 # [6] "De $420.001 a $470.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==7] <-(470001 +510000 )/2 # [7] "De $470.001 a $510.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==8] <-(510001 +560000 )/2 # [8] "De $510.001 a $560.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==9] <-(560001 +610000 )/2 # [9] "De $560.001 a $610.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==10]<-(610001 +670000 )/2 # [10] "De $610.001 a $670.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==11]<-(670001 +730000 )/2 # [11] "De $670.001 a $730.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==12]<-(730001 +800000 )/2 # [12] "De $730.001 a $800.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==13]<-(800001 +890000 )/2 # [13] "De $800.001 a $890.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==14]<-(890001 +980000 )/2 # [14] "De $890.001 a $980.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==15]<-(980001 +1100000)/2 # [15] "De $980.001 a $1.100.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==16]<-(1100001+1260000)/2 # [16] "De $1.100.001 a $1.260.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==17]<-(1260001+1490000)/2 # [17] "De $1.260.001 a $1.490.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==18]<-(1490001+1850000)/2 # [18] "De $1.490.001 a $1.850.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==19]<-(1850001+2700000)/2 # [19] "De $1.850.001 a $2.700.000 mensuales liquidos"
elsoc$inghogar_t[elsoc$inghogar_t==20]<-(2700000) # [20] "Mas de $2.700.000 a mensuales liquidos"Paso 2: En el caso de no tener información, remplazar por la media del tramo
elsoc$inghogar_i <- ifelse(test = (is.na(elsoc$inghogar)), #¿existen NA en ingresos?
yes = elsoc$inghogar_t, #VERDADERO, remplazar con la media del tramo
no = elsoc$inghogar) #FALSE, mantener la variable original.
elsoc$inghogar_i <- set_label(elsoc$inghogar_i,"Ingreso total del hogar (imputada)")Paso 3: Comparamos la variable original con la nueva
sjmisc::descr(elsoc[,c("inghogar","inghogar_i")],
show =c("label", "n", "NA.prc", "mean", "md","sd")) %>% knitr::kable(digits = 2)| var | label | n | NA.prc | mean | sd | md |
|---|---|---|---|---|---|---|
| inghogar | Ingreso total del hogar | 3080 | 17.82 | 678842.5 | 781003.9 | 500000 |
| inghogar_i | Ingreso total del hogar (imputada) | 3557 | 5.10 | 668539.5 | 752608.2 | 480000 |
Vemos que pasamos de tener 17,82% de datos perdidos a un 5,1%, es decir recuperamos un 12,72% de los casos que antes tenían datos perdidos en la variable ingreso. Con estos datos podemos calcular el ingreso per capita del hogar, empleando la variable habitantes del hogar (tamhogar).
elsoc$ing_pcap <- elsoc$inghogar_i/elsoc$tamhogar
elsoc$ing_pcap <- set_label(elsoc$ing_pcap,"Ingreso per cápita del hogar")sjmisc::descr(elsoc[,c("inghogar","inghogar_i","tamhogar","ing_pcap")],
show =c("label", "n", "NA.prc", "mean", "md","sd")) %>% knitr::kable(digits = 2)| var | label | n | NA.prc | mean | sd | md | |
|---|---|---|---|---|---|---|---|
| 2 | inghogar | Ingreso total del hogar | 3080 | 17.82 | 678842.52 | 781003.92 | 500000.0 |
| 3 | inghogar_i | Ingreso total del hogar (imputada) | 3557 | 5.10 | 668539.54 | 752608.16 | 480000.0 |
| 4 | tamhogar | Habitantes del hogar | 3741 | 0.19 | 3.16 | 1.57 | 3.0 |
| 1 | ing_pcap | Ingreso per cápita del hogar | 3552 | 5.23 | 263057.71 | 350338.36 | 166666.7 |
Vemos que la variable tamhogar posee un 0,19% de datos perdidos, por lo cual, al calcular el ingreso per cápita, vemos que el porcentaje de casos sin información en la nueva variable aumenta levemente a un 5,23%.
Ingresos como variable categórica
Teniendo el ingreso per cápita del hogar, podemos calcular categorías de ingresos tales como los quintiles (o deciles). Por lo tanto, podemos clasificar a los individuos según sus ingresos en una variable categórica.
El procedimiento es el siguiente:
elsoc$quintile<- dplyr::ntile(x = elsoc$ing_pcap,
n = 5) # n de categorias, para quintiles usamos 5
elsoc$quintile <- factor(elsoc$quintile,c(1,2,3,4,5), c("Quintil 1","Quintil 2","Quintil 3","Quintil 4","Quintil 5"))
elsoc %>%
group_by(quintile) %>%
summarise(n=n(),
Media=mean(ing_pcap,na.rm = T),
Mediana=median(ing_pcap,na.rm = T)) %>%
knitr::kable()| quintile | n | Media | Mediana |
|---|---|---|---|
| Quintil 1 | 711 | 62859.09 | 66666.67 |
| Quintil 2 | 711 | 112218.97 | 111250.12 |
| Quintil 3 | 710 | 167748.23 | 166666.67 |
| Quintil 4 | 710 | 262710.27 | 250000.50 |
| Quintil 5 | 710 | 710246.41 | 500000.00 |
| 196 |
En la tabla podemos observar que la variable quintile posee 5 grupos de tamaño equivalente. Además, agregamos la media y la mediana de los ingresos para cada categoría para ilustrar que podemos tratar esta variable como categórica y ordinal.
Existe una última estrategia que podemos utilizar para recuperar ese 5,23% (n=196) de casos perdidos. Para esto, generamos una categoría adicional para los datos perdidos, es decir, recodificamos los NA para que se incluyan como una nueva categoría.
El procedimiento es el siguiente:
elsoc$quintilemiss <- factor(elsoc$quintile,ordered = T)
elsoc$quintilemiss <- ifelse(is.na(elsoc$quintilemiss),yes = 6,no = elsoc$quintilemiss)
elsoc$quintilemiss <- factor(elsoc$quintilemiss ,levels = c(1,2,3,4,5,6),labels = c("Quintil 1","Quintil 2","Quintil 3","Quintil 4","Quintil 5","Missing"))
elsoc %>% group_by(quintilemiss) %>% summarise(n=n())## # A tibble: 6 x 2
## quintilemiss n
## <fct> <int>
## 1 Quintil 1 711
## 2 Quintil 2 711
## 3 Quintil 3 710
## 4 Quintil 4 710
## 5 Quintil 5 710
## 6 Missing 196Teniendo una nueva categoría de ingresos, podemos recuperar estos casos para los posteriores análisis. A continuación, se llevaran a cabo una serie de análisis que nos permitirán comprar los resultados según distintas especificaciones y empleando distintas maneras de operacionalizar la variable ingresos.
Estimación
fit01<- lm(partpol~sexo+edad+ing_pcap+pospol,data=elsoc)
fit02<- lm(partpol~sexo+edad+quintile+pospol,data=elsoc)
fit03<- lm(partpol~sexo+edad+quintilemiss+pospol,data=elsoc)labs01 <- c("Intercepto","Sexo (mujer=1)","Edad","Ingreso per/cap","Centro (ref. derecha)","Izquierda","Idep./Ninguno",
"Quintil 2","Quintil 3","Quintil 4","Quintil 5",
"Quintil 2","Quintil 3","Quintil 4","Quintil 5","Quintil perdido")
htmlreg(list(fit01,fit02,fit03),doctype = FALSE,
custom.model.names = c("Modelo 1","Modelo 2","Modelo 3"),
custom.coef.names = labs01)| Modelo 1 | Modelo 2 | Modelo 3 | |
|---|---|---|---|
| Intercepto | 8.27*** | 7.94*** | 7.97*** |
| (0.14) | (0.16) | (0.16) | |
| Sexo (mujer=1) | 0.05 | 0.13 | 0.12 |
| (0.07) | (0.08) | (0.07) | |
| Edad | -0.04*** | -0.04*** | -0.04*** |
| (0.00) | (0.00) | (0.00) | |
| Ingreso per/cap | 0.00*** | ||
| (0.00) | |||
| Centro (ref. derecha) | -1.02*** | -1.04*** | -1.04*** |
| (0.10) | (0.10) | (0.10) | |
| Izquierda | -1.10*** | -1.12*** | -1.13*** |
| (0.11) | (0.11) | (0.11) | |
| Idep./Ninguno | -1.59*** | -1.58*** | -1.60*** |
| (0.10) | (0.10) | (0.10) | |
| Quintil 2 | 0.22 | 0.21 | |
| (0.11) | (0.11) | ||
| Quintil 3 | 0.51*** | 0.51*** | |
| (0.11) | (0.11) | ||
| Quintil 4 | 0.51*** | 0.50*** | |
| (0.11) | (0.11) | ||
| Quintil 5 | 0.89*** | 0.88*** | |
| (0.12) | (0.12) | ||
| Quintil perdido | 0.59*** | ||
| (0.18) | |||
| R2 | 0.17 | 0.17 | 0.17 |
| Adj. R2 | 0.16 | 0.17 | 0.17 |
| Num. obs. | 3475 | 3475 | 3656 |
| p < 0.001; p < 0.01; p < 0.05 | |||