Práctica 4. Regresión simple 2
Índice
Objetivo de la práctica
Basados en el cálculo de parámetros del modelo de regresión en la práctica anterior (intercepto y coeficiente de regresión o pendiente), en esta práctica nos abocamos a temas de ajuste, residuos y relación entre correlación y regresión. La práctica está basada en el ejemplo de Darlington & Hayes cap. 2 (The simple regression model), que utilizamos en clases.
Librerías
pacman::p_load(stargazer, ggplot2, dplyr,webshot)Datos
Los datos a utilizar son los mismos que los de la práctica 3, corresponden a un ejemplo ficticio de 23 casos (individuos) y sus datos en dos variables relacionadas con un juego: el número de veces que se ha jugado antes (X) y el número de puntos ganados (Y).
datos <- read.csv("https://multivariada.netlify.app/slides/03-regsimple1/tacataca.txt", sep="")
datos## id juegos_x puntos_y
## 1 1 0 2
## 2 2 0 3
## 3 3 1 2
## 4 4 1 3
## 5 5 1 4
## 6 6 2 2
## 7 7 2 3
## 8 8 2 4
## 9 9 2 5
## 10 10 3 2
## 11 11 3 3
## 12 12 3 4
## 13 13 3 5
## 14 14 3 6
## 15 15 4 3
## 16 16 4 4
## 17 17 4 5
## 18 18 4 6
## 19 19 5 4
## 20 20 5 5
## 21 21 5 6
## 22 22 6 5
## 23 23 6 6También desde esta misma dirección web se pueden bajar los datos y llamarlos localmente
Directorio de trabajo :Directorio de trabajo
Para el trabajo de análisis de datos se recomienda establecer claramente el directorio de trabajo, es decir, la carpeta que contiene los archivos de datos, los códigos y los resultados. Esta carpeta es el lugar donde uno se posiciona para hacer los análisis, llamar otros archivos y exportar archivos.
Para esto, varias opciones:
- en RStudio, Session > Set Working Directory > Choose Directory
- también vía consola con el comando
setwd(ruta-hacia-la-carpeta-local) - o también se puede trabajar en un directorio contenido o cerrado con Rprojects, ejemplo aquí: https://www.doctormetrics.com/r-projects/.
Si se quiere verificar en qué carpeta se está trabajando, comando getwd()
Con esto entonces, si los datos están guardados en la misma carpeta, entonces se llaman simplemente datos <- read.csv("tacataca.txt", sep=""). No se requiere dar la ruta completa justamente porque el programa ya sabe dónde uno está posicionado. Asimismo, al momento de guardar/exportar algún resultado, automáticamente quedará en la carpeta de trabajo.
Recordando la distribución de los datos y la recta de regresión:
g2=ggplot(datos, aes(x=juegos_x, y=puntos_y)) +
geom_point() +
geom_smooth(method=lm, se=FALSE)
g2
Grabar / exportar gráficos :Exportar gráficos Si se quiere grabar un gráfico para luego utilizarlo en algún documento fuera del entorno R, algunas alternativas:
- utilizar la función
ggsave(para gráficos ggplot)
ggsave("g2.png", g2)- más genéricamente, para guardar como imagen cualquier cosa que aparece en el visor de RStudio:
png(file = "g2.png") # se abre un archivo vacío
g2 # se genera el gráfico a guardar en el archivo
dev.off() # se cierra el archivo
El gráfico quedará grabado en el directorio de trabajo (ver arriba). Si se desea que se grabe en otra parte, dar la ruta completa hacia la carpeta correspondiente (“C:/[ruta-hacia-carpeta]/g2.png”)
Residuos
En el gráfico anterior vemos que la línea resume la relación entre X e Y que se denomina recta de regresión, caracterizada por un intercepto y una pendiente.
Claramente, esta recta es una simplificación que no abarca toda la variabilidad de los datos. Por ejemplo, para el sujeto cuya experiencia es haber jugado 1 vez y luego gana 3 puntos, esta línea predice exactamente su puntaje basado en su experiencia. Sin embargo, el sujeto que ha jugado 3 veces y saca 6 puntos se encuentra más lejos de la línea y por lo tanto esta línea o “modelo predictivo” no representa tan bien su puntaje.
Lo anterior tiene que ver con el concepto de residuos, que es la diferencia entre el valor predicho (o \(\widehat{Y}\)) y el observado \(Y\). Por lo tanto, la mejor recta será aquella que minimice al máximo los residuos.
El sentido de la recta que resume de mejor manera la relación entre dos variables es que minimice la suma de todos los residuos. Para realizar la suma de los residuos estos se elevan al cuadrado, lo que se denomina suma de residuos al cuadrado o \(SS_{residual}\) ya que como hay residuos positivos y negativos unos se cancelan a otros y la suma es 0. De la infinita cantidad de rectas que se pueden trazar, siempre hay una que tiene un valor menor de \(SS_{residual}\). Este procedimiento es el que da nombre al proceso de estimación: residuos cuadrados ordinarios, o OLS (Ordinary Least Squares).
Modelo y cálculo de parámetros
Como vimos la práctica anterior, el modelo de regresión entonces se relaciona con una ecuación de la recta, o recta de regresión, que se puede definir en términos simples de la siguiente manera:
\[\widehat{Y}=b_{0} +b_{1}X \]
reg1 <-lm(puntos_y ~juegos_x, data = datos)
reg1##
## Call:
## lm(formula = puntos_y ~ juegos_x, data = datos)
##
## Coefficients:
## (Intercept) juegos_x
## 2.5 0.5Podemos generar una tabla en un formato más publicable:
stargazer(reg1, type="text")##
## ===============================================
## Dependent variable:
## ---------------------------
## puntos_y
## -----------------------------------------------
## juegos_x 0.500***
## (0.132)
##
## Constant 2.500***
## (0.458)
##
## -----------------------------------------------
## Observations 23
## R2 0.405
## Adjusted R2 0.376
## Residual Std. Error 1.091 (df = 21)
## F Statistic 14.280*** (df = 1; 21)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01También es posible generar una tabla más resumida en formato publicable y visible en RStudio, que tiene la información de los parámetros de regresión (intercepto y pendiente), además se presenta el ajuste (R2, además de R2 ajustado- tema de próxima clase), y también información de inferencia (valores p), que también veremos más adelante.
sjPlot::tab_model(reg1, show.ci=FALSE)| puntos y | ||
|---|---|---|
| Predictors | Estimates | p |
| (Intercept) | 2.50 | <0.001 |
| juegos_x | 0.50 | 0.001 |
| Observations | 23 | |
| R2 / R2 adjusted | 0.405 / 0.376 | |
Grabar / exportar tablas :Exportar tablas
Muchas de las tablas producidas con R son en formato html, es decir, archivos para ser publicados en formato web. Por lo tanto, en general las tablas se graban primero como html, y luego se convierten a formato imagen con la librería webshot.
Para tablas generadas con stargazer
stargazer(reg1, type="html", out = "reg1.html")
webshot("reg1.html","reg1.png")Alternativamente, para tablas de regresión con sjPlot:
sjPlot::tab_model(reg1, show.ci=FALSE, file = "reg1_tab.html")
webshot("reg1_tab.html","reg1_tab.png")
Bondad de Ajuste: Residuos y \(R^{2}\)
A partir del método de Mínimos Cuadrados Ordinarios obtenemos una recta que describe un conjunto de datos minimizando las diferencias entre el modelo y la distribución de los datos mismos.
No obstante, incluso cuando se ajusta el mejor modelo siempre existirá un grado de imprecisión, representado por las diferencias entre los datos observados y los valores predichos por la recta de regresión.
La precisión de nuestro modelo se relaciona con el concepto de Bondad de Ajuste, y se evalúa a partir del estadístico \(R^2\).
En el siguiente apartado se puede observar la manera de calcular la predicción de Y (puntos_y) en base a X (juegos_x), y almacenarlos en la base de datos, con los respectivos residuos.
#summary(lm(puntos_y~juegos_x, data=datos))
#beta=0.5 intercepto=2.5
#Variable de valores predichos
datos$estimado<- (2.5 + datos$juegos_x*0.5)
# Alternativa por comando
#datos$estimado <- predict(reg1)
#Estimamos el residuo
datos$residuo <- datos$puntos_y - datos$estimado
# Alternativa por comando
#datos$residuo <- residuals(reg1)
datos %>% select(id, estimado, residuo)## id estimado residuo
## 1 1 2.5 -0.5
## 2 2 2.5 0.5
## 3 3 3.0 -1.0
## 4 4 3.0 0.0
## 5 5 3.0 1.0
## 6 6 3.5 -1.5
## 7 7 3.5 -0.5
## 8 8 3.5 0.5
## 9 9 3.5 1.5
## 10 10 4.0 -2.0
## 11 11 4.0 -1.0
## 12 12 4.0 0.0
## 13 13 4.0 1.0
## 14 14 4.0 2.0
## 15 15 4.5 -1.5
## 16 16 4.5 -0.5
## 17 17 4.5 0.5
## 18 18 4.5 1.5
## 19 19 5.0 -1.0
## 20 20 5.0 0.0
## 21 21 5.0 1.0
## 22 22 5.5 -0.5
## 23 23 5.5 0.5Suma de cuadrados y \(R^{2}\)
Usando la media como modelo podemos calcular las diferencias entre los valores observados y los valores predichos por la media.
- Suma Total de Cuadrados: La suma de las diferencias del promedio de Y al cuadrado (asociado al concepto de varianza de Y)
\[SS_{tot} = \sum(y-\bar{y})^2 \] Y calculamos
ss_tot<- sum((datos$puntos_y-mean(datos$puntos_y))^2); ss_tot## [1] 42- Suma de cuadrados de la regresión: se refiere a la suma de diferencias (al cuadrado) entre el valor estimado por el modelo de regresión y la media. Expresa cuanto de la varianza de Y alcanzamos a predecir con X
\[SS_{reg} = \sum(\hat{y}-\bar{y})^2\]
ss_reg<-sum((datos$estimado-mean(datos$puntos_y))^2) ; ss_reg## [1] 17- Suma de residuos al cuadrado: al contrario de el cálculo anterior, los residuos representan la parte de la varianza de
Yque no alcanzamos a abarcar con nuestro modelo de regresión. Es decir, reprsentan el error en la predicción (diferencia entre lo estimado por el modelo y el valor observado)
\[SS_{error} = \sum(y-\hat{y})^2\]
ss_err<- sum((datos$puntos_y - datos$estimado)^2);ss_err## [1] 25A partir de las sumas de cuadrados anteriores es posible calcular el estadístico \(R^{2}\)
\[R^2=\frac{SS_{reg}}{SS_{tot}}= 1- \frac{SS_{error}}{SS_{tot}}\]
#Opción 1
ss_reg/ss_tot## [1] 0.4047619#Opción 2
1-ss_err/ss_tot## [1] 0.4047619#por comando
summary(lm(puntos_y~juegos_x, data=datos))$r.squared## [1] 0.4047619Visualización
En la siguiente sección se presentan distintas formas de visualizar los residuos a partir del paquete ggplot2.
#Visualizacion
library(ggplot2)
ggplot(datos, aes(x=juegos_x, y=puntos_y))+
geom_smooth(method="lm", se=FALSE, color="lightgrey") +#Pendiente de regresion
geom_segment(aes(xend=juegos_x, yend=estimado), alpha = .2) + #Distancia entre estimados y datos en lineas
geom_point() + #Capa 1
geom_point(aes(y=estimado), shape =1) +
theme_bw()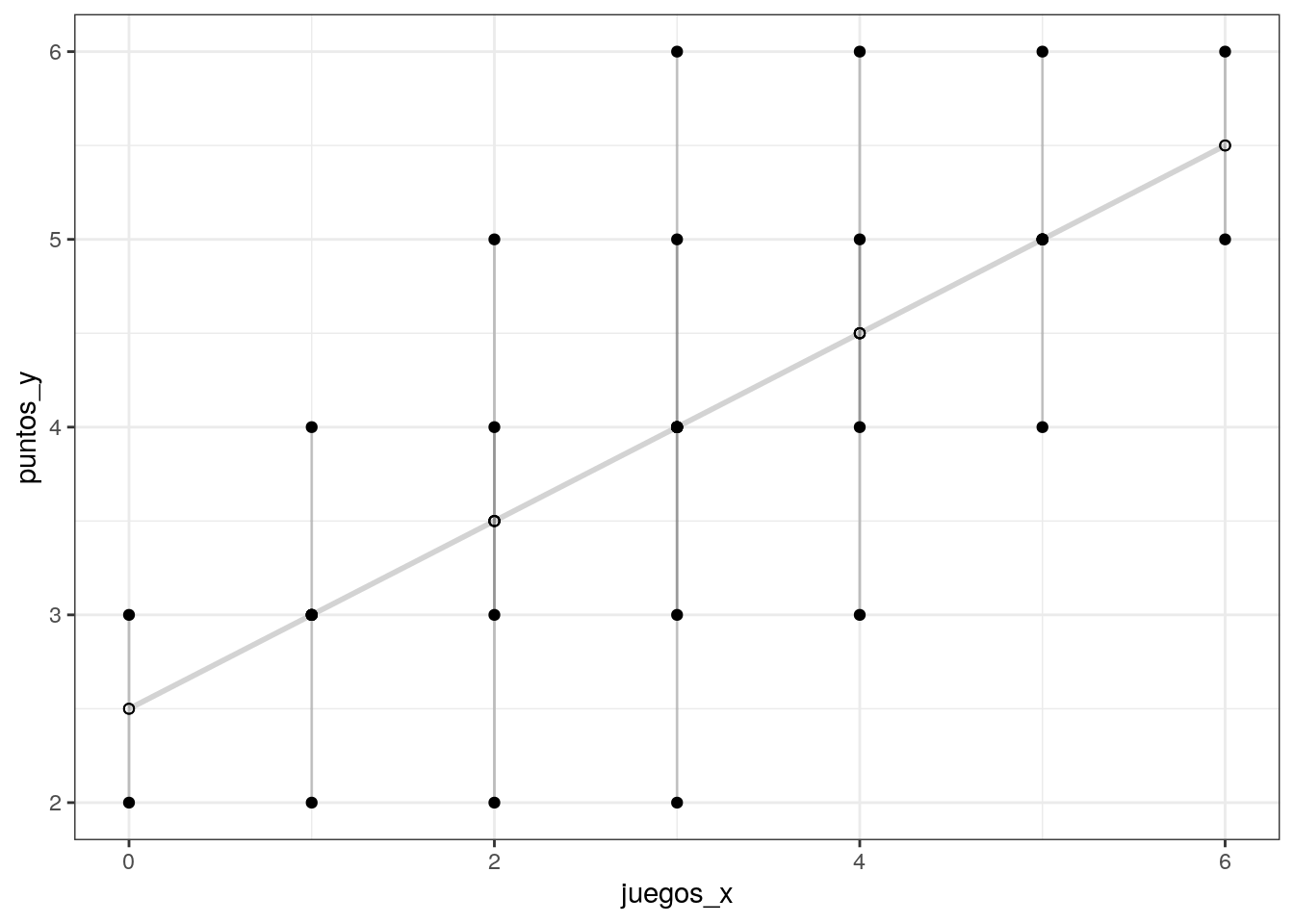
En esta segunda opción, se agrega tamaño y color a los residuos mayores:
ggplot(datos, aes(x=juegos_x, y=puntos_y))+
geom_smooth(method="lm", se=FALSE, color="lightgrey") +#Pendiente de regresion
geom_segment(aes(xend=juegos_x, yend=estimado), alpha = .2) + #Distancia entre estimados y datos en lineas
geom_point(aes(color = abs(residuo), size = abs(residuo))) + #tamaño de residuoes
scale_color_continuous(low = "black", high = "red") + # color de los residuos
guides(color = FALSE, size = FALSE) +
geom_point(aes(y=estimado), shape =1) +
theme_bw()
El coeficiente de Regresión versus el coeficiente de correlación
Tanto \(r_{xy}\) y \(\beta_1\) son medidas de la relación entre X e Y. Ellas estan relacionadas con la formula de:
\[\beta_1= r_{xy}(S_y/S_x)\]
Es decir:
beta<-cor(datos$juegos_x,datos$puntos_y)*(sd(datos$puntos_y)/sd(datos$juegos_x));beta## [1] 0.5reg1$coefficients[2] #llamamos al coeficiente beta (en posición 2) en el objeto reg1## juegos_x
## 0.5Del mismo modo existe una relación entre \(r_{xy}\) y \(R^2\)
#Correlación (Pearson) entre juegos_x y puntos_y (r)
cor(datos$juegos_x,datos$puntos_y)## [1] 0.636209#Correlación entre juegos_x y puntos_y al cuadrado.
(cor(datos$juegos_x,datos$puntos_y))^2## [1] 0.4047619La correlación entre X e Y es la misma que entre Y e X,
cor(datos$juegos_x,datos$puntos_y)## [1] 0.636209cor(datos$puntos_y,datos$juegos_x)## [1] 0.636209… mientras la regresión entre X e Y no es la misma que entre Y e X
lm(datos$puntos_y~datos$juegos_x)$coefficients## (Intercept) datos$juegos_x
## 2.5 0.5lm(datos$juegos_x~datos$puntos_y)$coefficients## (Intercept) datos$puntos_y
## -0.2380952 0.8095238Reporte de progreso
Completar el reporte de progreso aquí.
Archivo de código
El archivo de código R de esta práctica se puede descargar aquí