Verificación y descriptivos

Verificamos si los datos fueron correctamente cargados con View, también la dimensión de la base de datos con dim, y la naturaleza de las variables con sapply :

View(datos)
dim(datos)
sapply(datos, class)

Tenemos entonces tres columnas:

• id: número único que identifica a cada sujeto

• juegos_x: número de veces que ha jugado previamente

• puntos_y: numero de puntos que obtuvo en el juego actual

Generamos una tabla de descriptivos básicos con lo aprendido en la práctica de descripción de datos:

Y para publicar, usando la librería stargazer

stargazer(datos, type = "text")

## 
## ======================================================
## Statistic N   Mean  St. Dev. Min Pctl(25) Pctl(75) Max
## ------------------------------------------------------
## id        23 12.000  6.782    1    6.5      17.5   23 
## juegos_x  23 3.000   1.758    0     2        4      6 
## puntos_y  23 4.000   1.382    2     3        5      6 
## ------------------------------------------------------

En la tabla vemos los estadísticos básicos de las variables juegos y puntos, y además aparece la variable id, que es el identificador y por lo tanto no tiene sentido que salga en la tabla. Para corregir, seleccionamos las variables de interés de datos con el operador pipa %>% operador pipa %>%. Este operador permite unir distintas funciones en una misma línea de código, y es muy utilizado por librerías de manejo de datos como dplyr. Por ejemplo, ahora la instrucción es “de la base de datos datos” %>% “selecciona solo las columnas juegos y puntos”:

stargazer(datos %>% select(juegos_x,puntos_y) , type = "text")

## 
## =====================================================
## Statistic N  Mean  St. Dev. Min Pctl(25) Pctl(75) Max
## -----------------------------------------------------
## juegos_x  23 3.000  1.758    0     2        4      6 
## puntos_y  23 4.000  1.382    2     3        5      6 
## -----------------------------------------------------

Experiencia en juegos y puntuación

La pregunta que nos hacemos para este ejercicio de demostración es: ¿tiene relación la experiencia previa (juegos jugados previamente) con el desempeño actual (puntos obtenidos)?

Veamos un gráfico de nube de puntos / scatter de ambas variables. Para eso, primero cargamos la librería ggplotde R. Recordar que hay que instalarla primero si es que no se ha hecho previamente con install.packages("ggplot")ggplot.

g=ggplot(datos, aes(x=juegos_x, y=puntos_y)) +
  geom_point()
g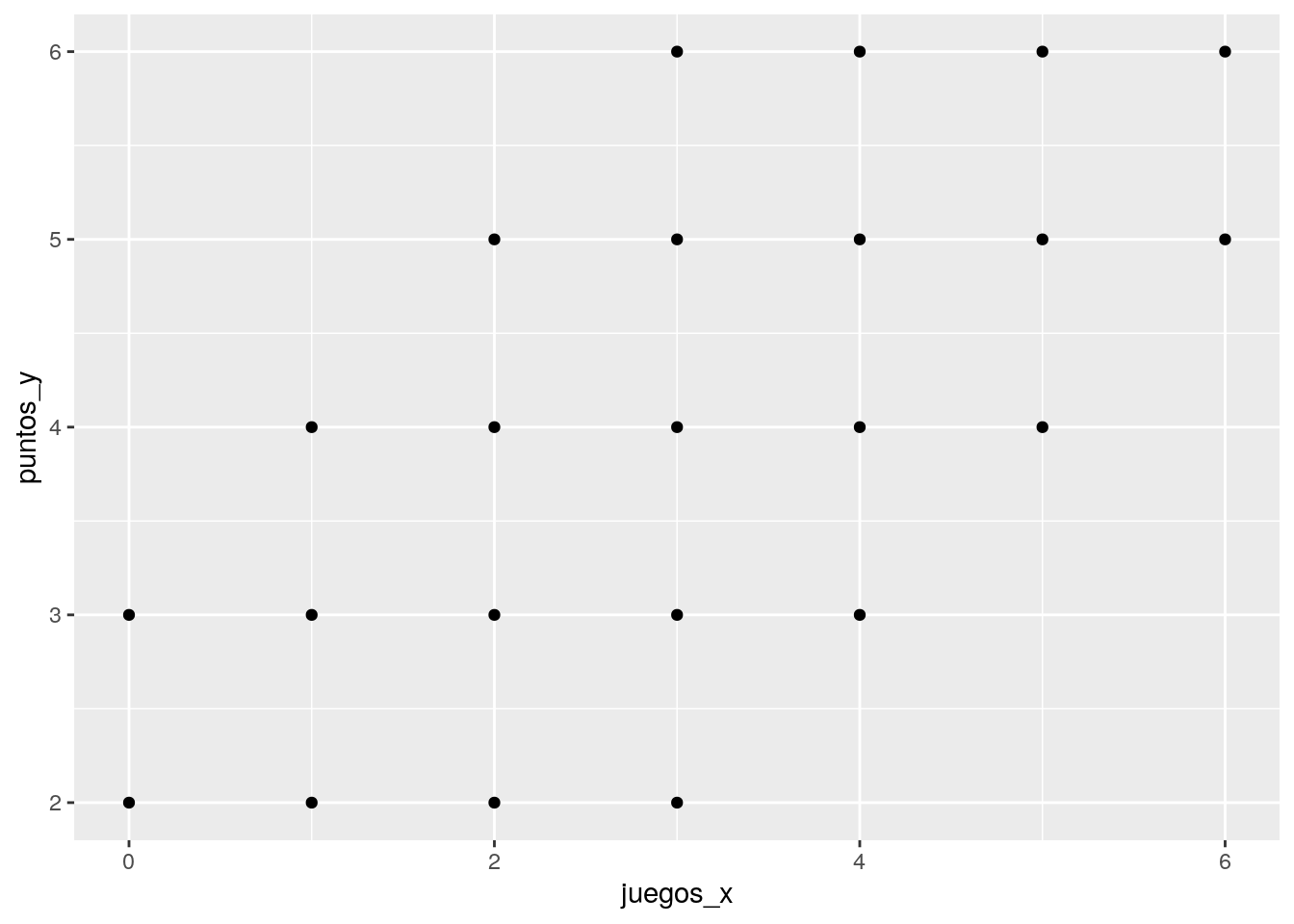

Primero, sobre librerías y visualización: lo que hicimos fue crear un objeto gráfico scatterplot g con la librería ggplot..

En términos de correlación se observa una posible asociación positiva, que podemos corroborar con la función cor:

cor(datos$juegos_x,datos$puntos_y)

## [1] 0.636209

Tenemos una correlación positiva (dirección de la relación) y de un tamaño de efecto grande (magnitud de la relación), para ciencias sociales. Es decir, existe una asociación positiva entre ambas variables: a medida que aumenta la experiencia en juegos, aumentan también los puntos obtenidos en el partido de taca taca. Ahora bien, ¿cómo se relaciona más específcamente la experiencia en juegos con los puntos obtenidos posteriormente?

Medias condicionales

Antes de avanzar desde la correlación al método de regresión es importante conocer el concepto de media condicional.

Como sabemos el promedio de Y (puntos) es 4. Es decir, si conocemos a algún individuo que pertence al grupo de “datos”, sabemos que su puntaje se encuentra probablemente cercano a 4. ¿Podemos mejorar nuestra estimación utilizando el puntaje de X? Como lo conocemos, si el sujeto nos dice que ha jugado antes 6 veces, dada la información que conocemos probablemente vamos a estimar un puntaje superior de puntos, tal vez más cercano a 6.

Lo que estamos haciendo es utilizar la información que conocemos de X para dar una estimación de Y, que sea más precisa que el promedio bruto.

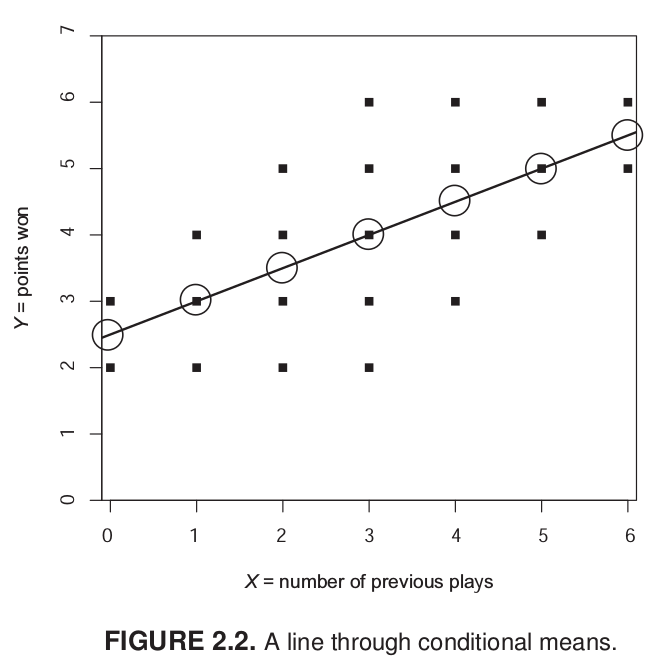
Mirando el gráfico de nube de puntos, sabemos que tres personas han jugado antes una vez, pero una de ellas tuvo 2 puntos, otra 3 y otra 4. Con estos datos podemos calcular la media de Y para X=1, que sería igual a 3. En otras palabras, la media condicional de Y cuando X=1 es 3. Con esto, uno podría calcular la media condicional para cada punto de X y hacer una estimación más precisa de Y. Sin embargo, este proceso todavía no nos permite generalizar más eficientemte la relación entre X e Y.

¿Cuántos puntos (Y) se obtienen según la experiencia previa de juego (X)? Esta pregunta nos conduce al cálculo de una recta que atraviese los puntos y que generalice la relación entre X e Y:

g2=ggplot(datos, aes(x=juegos_x, y=puntos_y)) +
  geom_point() +
  geom_smooth(method=lm, se=FALSE)
g2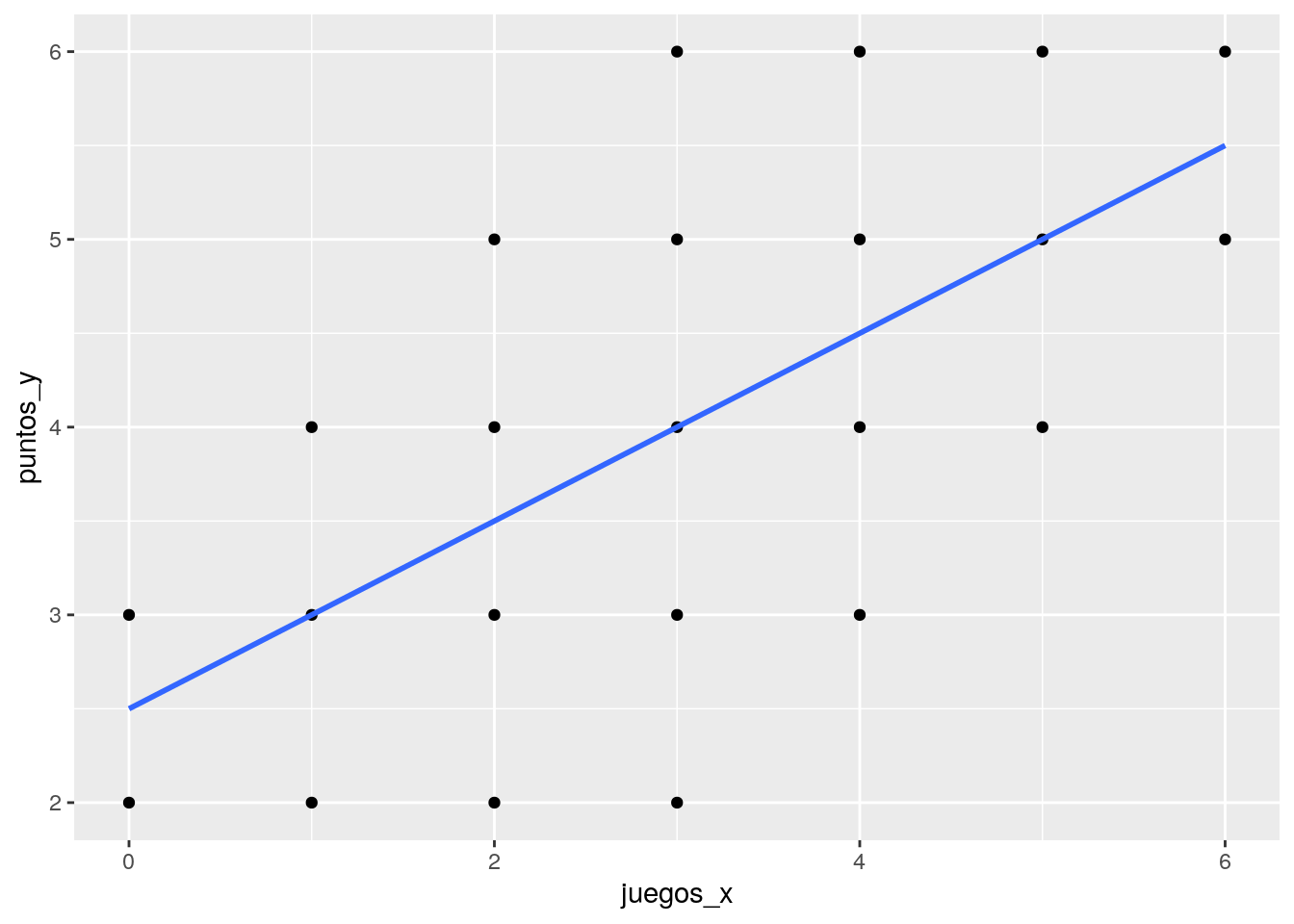

Residuos

En el gráfico anterior vemos que la línea resume la relación entre X e Y, pero claramente es una simplificación que no abarca toda la variabilidad de los datos.

Por ejemplo, para el sujeto cuya experiencia es haber jugado 1 vez y luego gana 3 puntos, esta línea predice exáctamente su puntaje basada en su experiencia. Sin embargo, el sujeto que ha jugado 3 veces y saca 6 puntos se encuentra más lejos de la línea y por lo tanto esta línea o “modelo predictivo” no representa tan bien su puntaje. A esto se refieren los residuos, que es la diferencia entre el valor predicho (o \(\widehat{Y}\)) y el observado \(Y\), siendo los valores predichos de Y los que pasan por la recta a la altura de cada valor de X. Por lo tanto, la mejor recta será aquella que minimice al máximo los residuos.

El sentido de la recta que resume de mejor manera la relación entre dos variables es que minimice la suma de todos los residuos. ¿Cómo realizar este procedimiento?

• Para realizar la suma de los residuos estos se elevan al cuadrado, lo que se denomina Suma de residuos al cuadrado o \(SS_{residual}\). Se eleva al cuadrado ya que como hay residuos positivos y negativos, unos cancelarían a otros y la suma seía 0, tal como sucede en la formula de la varianza.

• De la infinita cantidad de rectas que se pueden trazar, siempre hay una que tiene un valor menor de \(SS_{residual}\). Este procedimiento es el que da nombre al proceso de estimación: mínimos (residuos) cuadrados ordinarios, o OLS (Ordinary Least Squares).

Modelo de regresión y cálculo de parámetros

El nombre regresión hace alusión a investigaciones sobre estaturas de padres e hij_s en el S.XIX. La estatura de hij_s de padres muy altos es en promedio menor, y si sus padres son baj_s, es mayor (en comparación con sus padres). Este fenómeno se conoce como “regresión hacia el promedio”

El modelo de regresión se representa con una ecuación de la recta, o recta de regresión. Esta recta representa los valores predichos para Y según los distintos valores de X:

\[\begin{equation} \widehat{Y}=b_{0} +b_{1}X \tag{1} \end{equation}\]

Donde

• \(\widehat{Y}\) es el valor estimado/predicho de \(Y\)
• \(b_{0}\) es el intercepto de la recta (el valor de Y cuando X es 0)
• \(b_{1}\) es el coeficiente de regresión, que nos dice cuánto aumenta Y por cada punto que aumenta X (pendiente)

Cálculo de los parámetros del modelo de regresión

\(b_{1}\), o comunmente llamado “beta de regresión” se obtiene de la siguiente manera:

\[\begin{equation} b_{1}=\frac{Cov(XY)}{VarX} \tag{2} \end{equation}\]

En términos más suntantivos se puede entender como qué parte de la covariación que hay entre X e Y se relaciona con (la varianza de) X. Especificando la fórmula:

\[\begin{equation} b_{1}=\frac{\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {n-1}}{\frac{\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})} {n-1}} \tag{3} \end{equation}\]

Y simplificando

\[\begin{equation} b_{1}=\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})} \tag{4} \end{equation}\]

Como sabemos, la base para todos estos cálculos es el valor de cada variable menos su promedio. Vamos a crear un vector en nuestra base de datos difx=\(x-\bar{x}\) y dify=\(y-\bar{y}\)

datos$difx=datos$juegos_x-mean(datos$juegos_x)
datos$dify=datos$puntos_y-mean(datos$puntos_y)

Y ahora con esto podemos obtener la diferencia de productos cruzados dif_cru=\((x-\bar{x})*(y-\bar{y})\), así como la diferencia de X de su promedio al cuadrado SSx=\((x-\bar{x})^2\)

datos$difcru=datos$difx*datos$dify
datos$difx2=datos$difx^2
datos

##    id juegos_x puntos_y difx dify difcru difx2
## 1   1        0        2   -3   -2      6     9
## 2   2        0        3   -3   -1      3     9
## 3   3        1        2   -2   -2      4     4
## 4   4        1        3   -2   -1      2     4
## 5   5        1        4   -2    0      0     4
## 6   6        2        2   -1   -2      2     1
## 7   7        2        3   -1   -1      1     1
## 8   8        2        4   -1    0      0     1
## 9   9        2        5   -1    1     -1     1
## 10 10        3        2    0   -2      0     0
## 11 11        3        3    0   -1      0     0
## 12 12        3        4    0    0      0     0
## 13 13        3        5    0    1      0     0
## 14 14        3        6    0    2      0     0
## 15 15        4        3    1   -1     -1     1
## 16 16        4        4    1    0      0     1
## 17 17        4        5    1    1      1     1
## 18 18        4        6    1    2      2     1
## 19 19        5        4    2    0      0     4
## 20 20        5        5    2    1      2     4
## 21 21        5        6    2    2      4     4
## 22 22        6        5    3    1      3     9
## 23 23        6        6    3    2      6     9

Y con esto podemos obtener la suma de productos cruzados y la suma de cuadrados de X

sum(datos$difcru)

## [1] 34

sum(datos$difx2)

## [1] 68

Reemplazando en la fórmula

\[b_{1}=\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})}=\frac{34}{68}=0.5\]

Y con esto podemos obtener el valor de \(b_{0}\)

\[b_{0}=\bar{Y}-b_{1}\bar{X}\] \[b_{0}=4-(3 * 0.5)=2.5\]

Completando la ecuación:

\[\bar{Y}=2.5+0.5X\]

Esto nos permite estimar el valor de \(Y\) (o su media condicional) basado en el puntaje \(X\). Por ejemplo, cuál es el valor estimado de \(Y\) dado \(X=5\)?