Índice
Presentación
Esta práctica tiene que ver con poner en cuestión la calidad de nuestros modelos de regresión. Si bien en la estimación tenemos información sobre el ajuste genera según el R2, existen una serie de aspectos que podrían estar afectando nuestra estimación y haciendo que nuestro modelo no represente de buena manera las asociaciones entre las variables.
La siguiente práctica tiene el objetivo de introducir a los estudiantes en los supuestos y robustez del modelo de regresión, así como también las posibles alternativas de transformación de variables para corregir las estimaciones cuando los supuestos no se cumplen. Para ello, utilizaremos los datos de la encuesta MOVID-IMPACT con el objetivo de analizar los determinantes de la Fatiga pandémica
Librerías
pacman::p_load(tidyverse, magrittr,
summarytools, sjPlot, performance, see)Datos
MOVID-IMPACT es una encuesta transversal telefónica realizada por el equipo CoV-IMPACT-C del proyecto ANID N°960.El objetivo de la encuesta es conocer el impacto en la salud y socioeconómico que ha tenido la pandemia sobre la población chilena.
Se cargan los datos directamente desde el sitio de la encuesta
movid <- haven::read_dta(url("https://movid-impact.netlify.app/input/data/MOVID-IMPACT.dta"))Procesamiento
Filtraremos los datos solo con la información de los encuestados, seleccionaremos las variables de interés para el práctico y recodificaremos los casos perdidos (para repasar, ver tutorial de dplyr)
movid_proc <- movid %>%
group_by(id_encuesta) %>% #Para calcular tamano de hogar
mutate(tamanohogar = n()) %>%
ungroup() %>%
filter(entrevistado == 1) %>% #Filtrar solo a entrevistados
select(sexo, edad, trabaja = g1,ingreso = g47_monto, tingreso= g48, tamanohogar, starts_with("c2"), fatiga = f5_3) %>% #Seleccionar variabes
mutate_at(vars(-tingreso), ~car::recode(.,"c(8,9) = NA")) %>%
mutate(tingreso = car::recode(tingreso,"c(98,99) = NA")) %>%
mutate_at(vars(sexo, trabaja, starts_with("c2"), tingreso, -fatiga), ~as_factor(.))Explorar datos
Los datos utilizados tienen 1261 observaciones y 11 variables, las cuales serán descritas en la siguiente tabla
Tabla N°1 Estadísticos descriptivos de base de datos procesadas de MOVID-IMPACT
view(dfSummary(movid_proc, headings = FALSE, method = "render"))Fuente: Elaboración propia en base a MOVID-IMPACT (n=909 casos)
| Variable | Etiqueta | Estadísticas / Valores | Frec. (% sobre válidos) | Gráfico |
|---|---|---|---|---|
| sexo [factor] |
Sexo | 1. Hombre 2. Mujer |
481 (38.1%) 780 (61.9%) |
IIIIIII IIIIIIIIIIII |
| edad [numeric] |
Edad | Media (d-s) : 48.8 (18.2) min < mediana < max: 18 < 48 < 96 RI (CV) : 30 (0.4) |
75 valores distintos | : . : : : : . . : : : : : : : . : : : : : : : : : : : : : : : : : |
| trabaja [factor] |
Durante la semana pasada, ¿trabajó al menos una hora, sin considerar los quehace | 1. Sí 2. No |
612 (48.5%) 649 (51.5%) |
IIIIIIIII IIIIIIIIII |
| ingreso [numeric] |
Monto de ingreso total de su hogar el mes de noviembre de 2020 | Media (d-s) : 679414.7 (836325.7) min < mediana < max: 0 < 4e+05 < 1.2e+07 RI (CV) : 450000 (1.2) |
151 valores distintos | : : : : : . |
| tingreso [factor] |
Tramo de ingreso total de su hogar el mes de noviembre de 2020 | 1. Menos de $200 mil pesos 2. Entre $200 y 350 mil peso 3. Entre $351 y 500 mil peso 4. Entre 501 y 800 mil pesos 5. Entre 801 mil y 1 millón 6. Entre 1 millón 201 mil y 7. Entre 2 millones y 5 mill 8. Más de 5 millones de peso 9. No sabe 10. No responde |
47 (22.5%) 57 (27.3%) 38 (18.2%) 35 (16.7%) 9 ( 4.3%) 15 ( 7.2%) 8 ( 3.8%) 0 ( 0.0%) 0 ( 0.0%) 0 ( 0.0%) |
IIII IIIII III III I |
| tamanohogar [integer] |
Media (d-s) : 2.8 (1.5) min < mediana < max: 1 < 3 < 14 RI (CV) : 2 (0.5) |
1 : 287 (23.0%) 2 : 321 (25.7%) 3 : 265 (21.2%) 4 : 222 (17.8%) 5 : 98 ( 7.8%) 6 : 38 ( 3.0%) 7 : 16 ( 1.3%) 10 : 1 ( 0.1%) 12 : 1 ( 0.1%) 14 : 1 ( 0.1%) |
IIII IIIII IIII III I |
|
| c2_1 [factor] |
Últimas 2 semanas: se ha sentido nervioso, ansioso o con los nervios de punta | 1. Nunca 2. Varios días 3. Más de la mitad de los dí 4. Casi todos los días 5. No sabe 6. No responde |
573 (45.7%) 389 (31.0%) 91 ( 7.3%) 200 (16.0%) 0 ( 0.0%) 0 ( 0.0%) |
IIIIIIIII IIIIII I III |
| c2_2 [factor] |
Últimas 2 semanas: No ha podido dejar de preocuparse o no ha podido controlar su | 1. Nunca 2. Varios días 3. Más de la mitad de los dí 4. Casi todos los días 5. No sabe 6. No responde |
629 (50.2%) 377 (30.1%) 101 ( 8.1%) 145 (11.6%) 0 ( 0.0%) 0 ( 0.0%) |
IIIIIIIIII IIIIII I II |
| c2_3 [factor] |
Últimas 2 semanas: Se ha sentido bajoneado, deprimido, irritable o desesperanzad | 1. Nunca 2. Varios días 3. Más de la mitad de los dí 4. Casi todos los días 5. No sabe 6. No responde |
529 (42.3%) 454 (36.3%) 104 ( 8.3%) 165 (13.2%) 0 ( 0.0%) 0 ( 0.0%) |
IIIIIIII IIIIIII I II |
| c2_4 [factor] |
Últimas 2 semanas: Ha sentido poco interés o placer al hacer las cosas | 1. Nunca 2. Varios días 3. Más de la mitad de los dí 4. Casi todos los días 5. No sabe 6. No responde |
679 (54.1%) 358 (28.5%) 89 ( 7.1%) 128 (10.2%) 0 ( 0.0%) 0 ( 0.0%) |
IIIIIIIIII IIIII I II |
| fatiga [haven_labelled, vctrs_vctr, double] |
Me siento cada vez más desmotivado para seguir las medidas de protección… | Media (d-s) : 2.8 (1.1) min < mediana < max: 1 < 2 < 5 RI (CV) : 2 (0.4) |
1 : 84 ( 6.8%) 2 : 588 (47.3%) 3 : 76 ( 6.1%) 4 : 432 (34.8%) 5 : 63 ( 5.1%) |
I IIIIIIIII I IIIIII I |
Introducción
2. Ajuste (post-hoc): implica abordar qué tan bien ajustan nuestros modelos con los datos utilizados. La bondad de ajuste implica que si trabajamos con una
- 2.1 Regresión lineal múltiple, analizaremos el \(R^2\) ajustado
- 2.2 Regresión logística, analizaremos el \(Pseudo\) \(R^2\) y los Criterios de Información \(BIC\) y \(AIC\) (ambos nos dicen cuánta información se está “perdiendo” con las variables que se ocupan en cada modelo. Por ello elegiremos el modelo que tenga un BIC y AIC más bajo)
3. Comparación: luego de que hacemos transformaciones a los modelos, una etapa importante para la selección de estos es compararlos. Para ello consideraremos toda la información que tenemos de ellos en su diagnóstico de pre y post hoc.
¿Cómo evaluar la robustez y ajuste de modelos en R?
En R existen diversas funciones para crear un diagnóstico de supuestos y de ajuste a nuestros modelos. Ahora bien, la gran parte de ello se desenvuelve en distintos paquetes, sobre todo considerando que, como vimos, no existen criterios únicos para evaluar la calidad de nuestros modelos (más aún cuando son su variable dependiente tiene un nivel distinto de medición).
La buena noticia es que el paquete performace reúne todas estas herramientas, y que los tres ejes de la calidad de los modelos también las distingue en una función para cada una.

Figura 2. paquete performance del proyecto easystats de Lüdecke et al. (2021)
Diagnóstico de la calidad de los modelos
Imaginemos que queremos analizar los determinantes de la Fatiga pandémica, y para ello estimaremos un modelo de regresión lineal.
model1 <- lm(as.numeric(fatiga) ~ c2_1 + c2_2 + c2_3 + c2_4 +
trabaja + sexo + edad + ingreso,
data = movid_proc)| Modelo 1 | |
|---|---|
| (Intercept) | 2.60*** |
| (0.14) | |
| c2_1Varios días | -0.17 |
| (0.10) | |
| c2_1Más de la mitad de los días | 0.23 |
| (0.16) | |
| c2_1Casi todos los días | -0.08 |
| (0.14) | |
| c2_2Varios días | -0.02 |
| (0.10) | |
| c2_2Más de la mitad de los días | -0.07 |
| (0.17) | |
| c2_2Casi todos los días | -0.10 |
| (0.15) | |
| c2_3Varios días | 0.19 |
| (0.10) | |
| c2_3Más de la mitad de los días | 0.23 |
| (0.17) | |
| c2_3Casi todos los días | 0.29 |
| (0.16) | |
| c2_4Varios días | 0.16 |
| (0.10) | |
| c2_4Más de la mitad de los días | 0.24 |
| (0.17) | |
| c2_4Casi todos los días | 0.32* |
| (0.16) | |
| trabajaNo | 0.06 |
| (0.08) | |
| sexoMujer | 0.02 |
| (0.08) | |
| edad | 0.00 |
| (0.00) | |
| ingreso | -0.00 |
| (0.00) | |
| R2 | 0.04 |
| Adj. R2 | 0.02 |
| Num. obs. | 917 |
| p < 0.001; p < 0.01; p < 0.05 | |
1. Robustez y supuestos
Los modelos de regresión tienen una serie de supuestos que se deben cumplir para que las estimaciones sean fidedignas.En esa sesión consideraremos los supuestos más esenciales: linealidad, normalidad de residuos, homogeneidad de la varianza, independencia de variables, multicolinealidad y casos influyentes (los primeros tres aplican solo para regresiones lineales).
Figura 3. Diferentes funciones de performance para evaluar robustez del modelo
1.1 Linealidad
Para la regresión lineal múltiple, un supuesto importante es que existe una relación lineal entre la variable dependiente e independiente.
Podemos saber si se cumple este supuesto a partir de un gráfico de dispersión de datos, que relacione la variable dependiente y la independiente, y verificar de manera “intuitiva” si la tendencia de esta relación se puede describir por una línea recta. El paquete performace nos permite hacer esto con su función check_model indicando en el argumento check = "ncv
check_model(model1, check = c("ncv", "linearity"))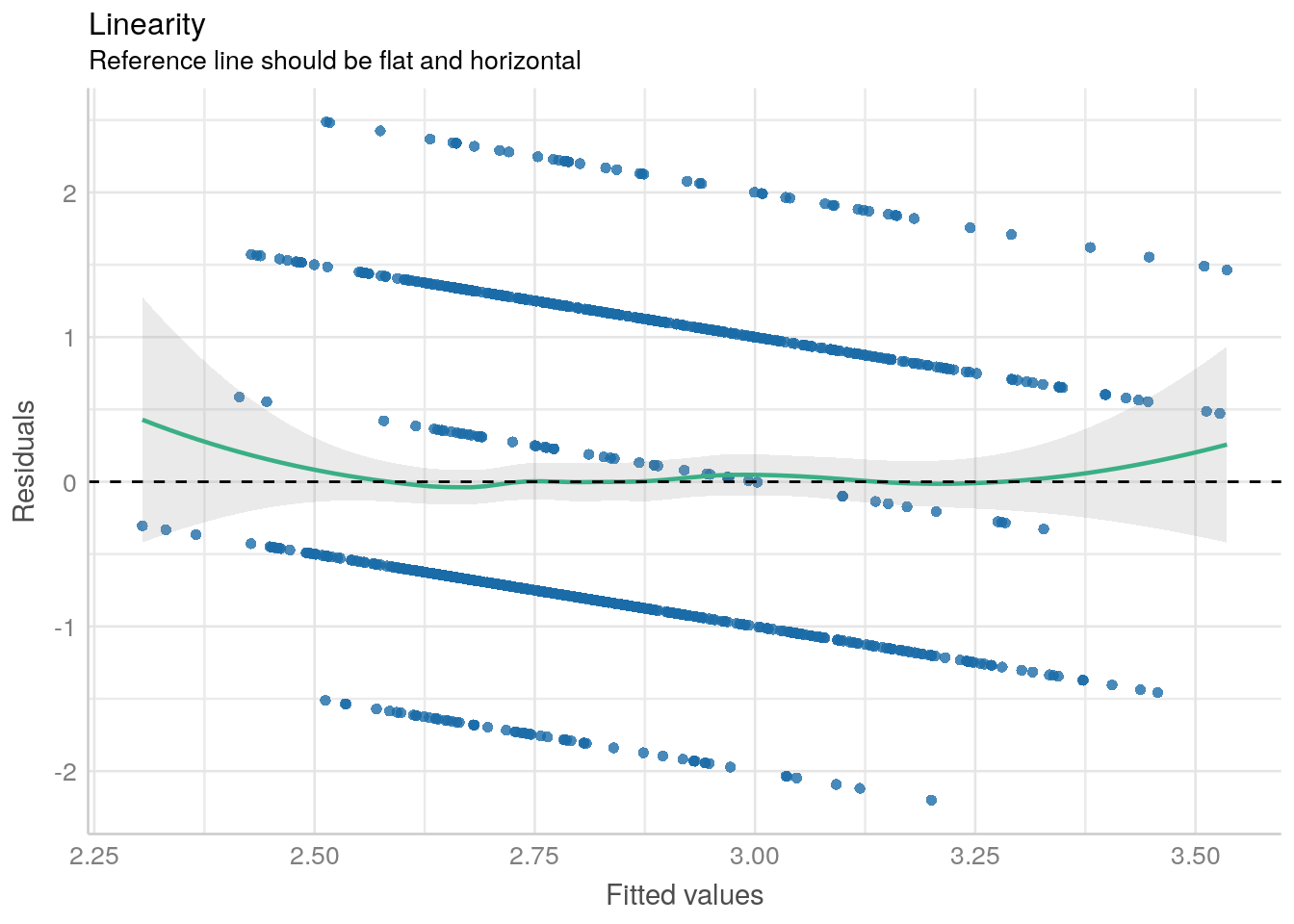
En este caso podemos notar claramente que no hay una relación lineal. En caso de que no sea claro, una forma numérica para chequear este supuesto es que el valor promedio de los residuos sea cero. Si esto no es así los residuos están sesgados sistemáticamente, entonces probable que el modelo no sea realmente lineal, y esta desviación de los residuos deba corregirse re-especificando (medir de otra manera la variable) algún término de la ecuación de regresión al cuadrado o al cubo. Un modo que se ocupa para testear la necesidad de esta re-especificación es el test RESET de Ramsey que indica que:
\(H_o\) cuando el modelo tiene algún término al cuadrado o cubo, la media de los residuos es cero. Es decir, que si no podemos rechazar \(H_0\), nuestro modelo está bien especificado (es decir, es lineal). Como en este caso es claro que se necesita respecificar el predictor elevamos edad al cuadrado. Imaginemos que es el caso
✔️ La línea de referencia es plana y horizontal
1.2 Homocedasticidad
Homoce ¿qué? Sí, homocedasticidad. Este concepto indica que los residuos se distribuyen de forma homogénea (por eso el sufijo homo). Como ya podrás haber notado este supuesto se vincula con el de linealidad
Al igual que la linealidad también puede comprobarse con un gráfico de dispersión entre la variable dependiente (\(Y\)) e independiente (\(X\)), donde podamos ver de manera clara la recta de regresión estimada y la distribución de los residuos. Aceptaremos el supuesto de homocedasticidad si la variación de los residuos es homogénea, es decir, no veremos un patrón claro y más bien se distribuirán de forma aleatoria. De manera gráfica veremos una nube de puntos que tiene una forma similar en todo el rango de las observaciones de la variable independiente.
Para comprobar el supuesto de homocedasticidad de manera más certera utilizaremos la prueba Breusch-Pagan Godfrey cuya hipótesis nula indica que
\(H_0\): La varianza de los residuos del modelo de regresión no es constante (heterocedasticidad)
En este caso, buscaremos que rechazar la \(H_0\). Esto implicaría que “en suma y resta” si bien hay residuos, estos tienen una variación homogénea en todos los tramos de la relación de la variable dependiente con la independiente.
A partir de la función check_heteroscedasticity verificaremos qué ocurre con la hipótesis nula
check_heteroscedasticity(model1)OK: Error variance appears to be homoscedastic (p = 0.494).
✔️ La varianza es homocedástica
1.3 Normalidad de residuos
Además de la linealidad (media 0), la homocedasticidad (varianza mínima y constante), el método de estimación de la regresión lineal (OLS o MCO en español) requiere asegurar una distribución normal de los residuos pues en caso contrario el modelo no es consistente a través de las variables y observaciones (esto significa que los errores no son aleteatorios).
Al igual que con los otros supuestos, la normalidad de los residuos se puede evaluar con métodos numéricos con pruebas que ya conocemos de otros cursos como la prueba de Shapiro-Wilk y Kolmogorov-Smirnov
A partir de la función check_normality utilizaremos la prueba Shapiro-Wilk para ver qué ocurre con la hipótesis nula a
check_normality(model1)Warning: Non-normality of residuals detected (p < .001).
⚠️ Los residuos no son normales
1.4 Independencia
Evidentemente si los residuos no siguen una distribución normal, es probable que estos no sean independientes entre sí. Esto significa que buscaremos que los errores asociados a nuestro modelo de regresión sean independientes. Para saber si se cumple ese criterio se utiliza la prueba de Durbin-Watson, donde la \(H_0\) supone que los residuos son independientes
A partir de la función check_autocorrelation utilizaremos la prueba Durbin-Watson para ver qué ocurre con la hipótesis nula a
check_autocorrelation(model1)Warning: Autocorrelated residuals detected (p = 0.010).
⚠️ Hay correlación entre los residuos
En síntesis sabemos la regresión lineal requiere de una relación lineal entre sus variables independientes y dependiente. Para ello no solo es importante chequear la distribución de los residuos, sino dos posibilidades que pueden tendenciar esa relación lineal: como casos influyentes en la muestra y predictores que están altamente relacionados. Revisaremos la última de estas
1.5 Multicolinealidad
La multicolinealidad es la relación de dependencia lineal fuerte entre más de dos predictores de un modelo.
El problema que produce es que será difícil cuantificar con exactitud el efecto de cada predictor sobre la variable dependiente, precisamente pues puede ocurrir que el efecto que una variable predictora tenga sobre el fenómeno que se busca estudiar dependa del valor de otra variable del modelo.
Para la regresión múltiple esto implica un problema pues suponemos que podemos “controlar” por el otro valor de la variable.
Esta relación endógena entre predictores la podemos examinar ante la existencia de altas correlaciones (lineales) entre variables. La aproximación numérica más utilizada es el VIF (factor de inflación de varianza) que indica hasta que punto la varianza de los coeficientes de regresión se debe a la colinealidad (o dependencia) entre otras variables del modelo.
Para evaluar esto ocuparemos el comando check_collinearity(). Como podemos ver en el gráfico, todos los valores son menores a 5 (como recomienda el paquete).
plot(check_collinearity(model1))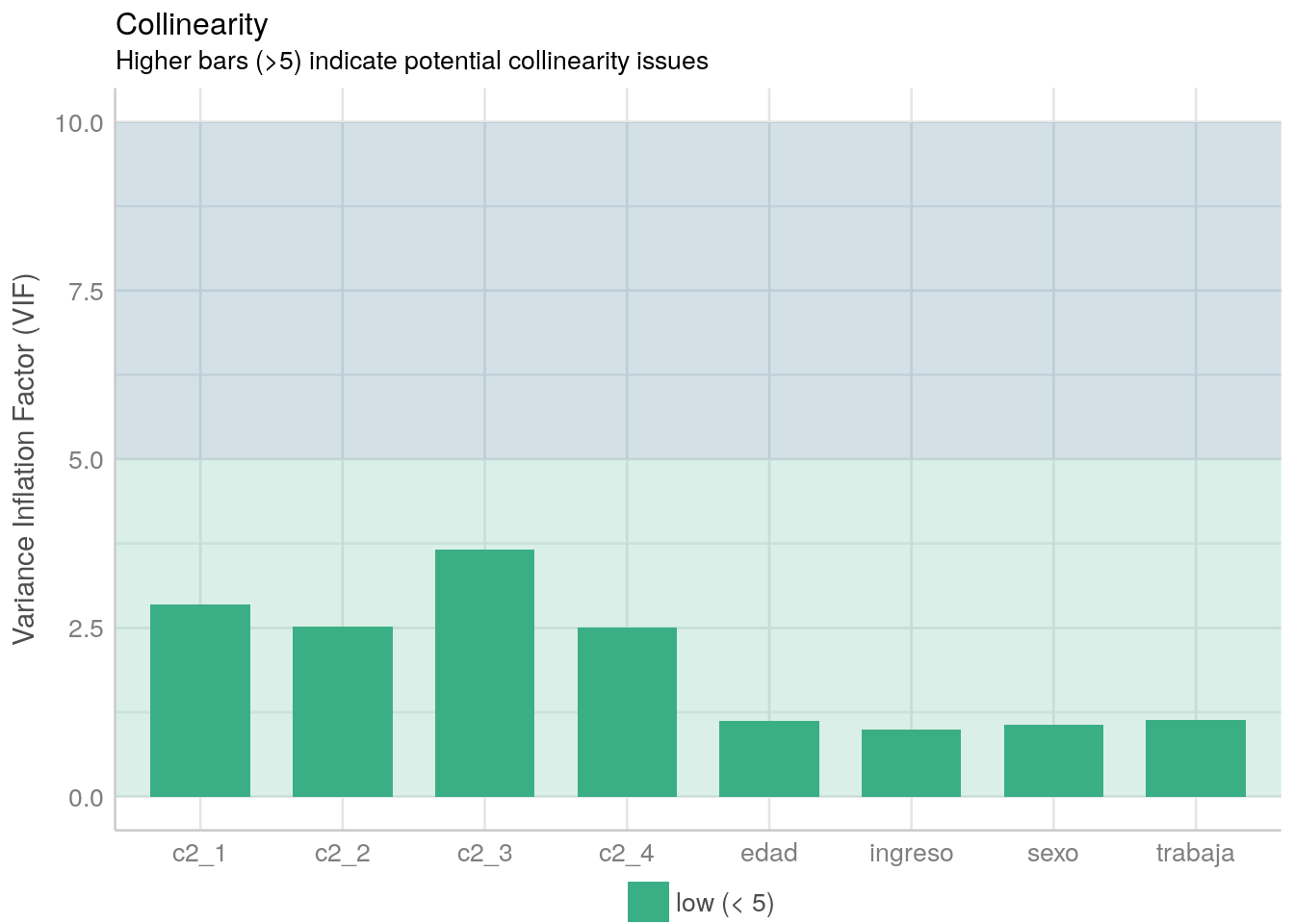
Ahora bien, dado que sabemos que las correlaciones en ciencias sociales nunca son tan altas, un criterio que se ocupa en nuestras disciplinas para evaluar multicolinealidad es es evitar valores del VIF mayores a 2.5.
check_collinearity(model1)Check for Multicollinearity
Low Correlation
Parameter VIF Increased SE c2_1 2.85 1.69 c2_2 2.51 1.59 c2_3 3.66 1.91 c2_4 2.51 1.58 trabaja 1.13 1.06 sexo 1.06 1.03 edad 1.13 1.06 ingreso 1.00 1.00
⚠️ Como podemos ver los ítems del módulo de salud mental tienen todos valores sobre 2.5. Como veremos en el segundo apartado de esta sesión, las recomendaciones son o eliminar alguno de los predictores o evaluar si es que estas variables más bien son parte de un mismo constructo (y para ello las correlacionaremos)
1.6 Casos influyentes
Un último supuesto que revisaremos, y es el que probablemente parte del que más nos enfrentamos en las ciencias sociales, son los casos influyentes (también llamados en inglés, outliers). Un ejemplo claro de esto son las variables como ingresos, donde muchas veces tenemos casos extremos con muy bajos salarios y otros muy altos, y que pueden tendenciar nuestras rectas de regresión pese a que no es evidente una relación lineal(o algún tipo de relación) entre la variable independiente y dependiente.
Para verificar si un “caso es influyente” examinaremos si la ausencia o presencia de ese caso genera un cambio importante en la estimación del modelo de regresión. Este enfoque se aborda a partir del cálculo de la Distancia de Cook (Cook,1977)
Primero podemos graficar la influencia de los casos con check_outliers() dentro de un plot()
plot(check_outliers(model1))
Luego para verificar si la ausencia o presencia de eliminar algunos de estos casos que presentan mayor distancia producen una diferencia significativa en la estimación del modelo, realizamos
check_outliers(model1)OK: No outliers detected.
✔️ No hay outliers
2. Ajuste del modelo
Sabemos por la práctica 5 que podemos evaluar qué tan bien ajustan nuestros modelos con los datos utilizados. Sabemos que:
2.1 Si trabajamos una regresión lineal: el \(R^2\) ajustado
2.2 Si trabajamos una regresión logística: Pseudo \(R^2\) y los Criterios de Información BIC y AIC (ambos nos dicen cuánta información se está “perdiendo” con las variables que se ocupan en cada modelo. Por ello elegiremos el modelo que tenga un BIC y AIC más bajo).
performance::model_performance(model1) %>%
print_md() #print_md() nos permite hacer tablas en buen formato| AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma |
|---|---|---|---|---|---|
| 2817.44 | 2904.22 | 0.04 | 0.02 | 1.10 | 1.11 |
Es probable que estos ajustes coincidan mejor con el fenómeno que queremos analizar una vez que hicimos el chequeo de supuestos. Esto no implica necesariamente que el ajuste mejore, sino que seremos más fieles a la información que realmente nos están otorgando las variables.
Ya hemos dado una serie de recomendaciones de transformaciones a las variables para manejar el problema de supuestos. En la siguiente tabla sistematizamos algunas de ellas.
| Problema | Soluciones posibles |
|---|---|
| No linealidad de variable dependiente e independiente | Transformar predictor al cuadrado o cubo |
| Logaritmizar variable dependiente | |
| Dicotomizar variable dependiente | |
| No normalidad de residuos | Transformar predictor al cuadrado o cubo |
| Logaritmizar variable dependiente | |
| Dicotomizar variable dependiente | |
| Heterocedasticidad de residuos | Calcular errores estándares robustos |
| Dependencia entre predictores | Interacción entre variables |
| Variables no observadas | |
| Multicolinealidad | Creación de índices |
| Interacción entre variables | |
| Eliminar variables | |
| Casos influyentes | Eliminar casos influyentes |
Ahora mostraremos de manera operativa como ejecutarlas.
2.1 Transformar predictor al cuadrado o cubo
Si estamos ante problemas de linealidad, indicamos que el término cuadrático o al cubo de algún predictor produce que la media de los residuos sea 0. Por lo general, por su distribución, esta variable es edad.
movid_proc <- movid_proc %>% mutate(edad2 = (edad)^2)2.2 Logaritmizar variable dependiente
Otro caso similar ocurre con ingresos, donde lo que se hace frecuentemente es transformar ingresos en un logaritmo de ingresos (log(ingresos)).
2.2.1 Recuperar casos perdidos
¡Pero antes! Es común que en las encuestas sociales cierta variables posean una alta proporción de datos perdidos. Un ejemplo común es en el reporte de los ingresos de los hogares o individuos. Esto generalmente puede generarse por características de la persona (eg. desempleado, estudiante) o por deseabilidad social (eg. personas de altos ingresos desisten de reportar). Por lo general, existen dos estrategias para solicitar que las personas reporten sus ingresos: (1) reporte directo del monto y (2) si la persona no reporta los ingresos, se le presenta la posibilidad de ubicar los ingresos del hogar en tramos.
movid_proc %>% select(ingreso, tingreso) %$%
print(dfSummary(., headings = FALSE, method = "render", varnumbers = F, lang = "es"))| Variable | Etiqueta | Estadísticas / Valores | Frec. (% sobre válidos) | Gráfico | Válido | Perdidos |
|---|---|---|---|---|---|---|
| ingreso [numeric] |
Monto de ingreso total de su hogar el mes de noviembre de 2020 | Media (d-s) : 679414.7 (836325.7) min < mediana < max: 0 < 4e+05 < 1.2e+07 RI (CV) : 450000 (1.2) |
151 valores distintos | : : : : : . |
942 (74.7%) |
319 (25.3%) |
| tingreso [factor] |
Tramo de ingreso total de su hogar el mes de noviembre de 2020 | 1. Menos de $200 mil pesos 2. Entre $200 y 350 mil peso 3. Entre $351 y 500 mil peso 4. Entre 501 y 800 mil pesos 5. Entre 801 mil y 1 millón 6. Entre 1 millón 201 mil y 7. Entre 2 millones y 5 mill 8. Más de 5 millones de peso 9. No sabe 10. No responde |
47 (22.5%) 57 (27.3%) 38 (18.2%) 35 (16.7%) 9 ( 4.3%) 15 ( 7.2%) 8 ( 3.8%) 0 ( 0.0%) 0 ( 0.0%) 0 ( 0.0%) |
IIII IIIII III III I |
209 (16.6%) |
1052 (83.4%) |
Si observamos la tabla de descriptivos para la variable ingreso del hogar (ingreso), tenemos un porcentaje 25,3% de datos perdidos. Por esta razón, emplearemos los datos disponibles en tingreso para recuperar información en los ingresos del hogar.
La estrategia posee los siguientes pasos:
- Paso 1: Calcular la media por cada tramo
- Paso 2: En el caso de no tener información, remplazar por la media del tramo
movid_proc <- movid_proc %>%
mutate(tingreso = case_when(tingreso == "Menos de $200 mil pesos" ~ 200000,
tingreso == "Entre $200 y 350 mil pesos" ~ 275000,
tingreso == "Entre $351 y 500 mil pesos" ~ 425500,
tingreso == "Entre 501 y 800 mil pesos" ~ 650500,
tingreso == "Entre 801 mil y 1 millón 200 mil pesos" ~ 1000500,
tingreso == "Entre 1 millón 201 mil y 2 millones de pesos" ~ 1600500,
tingreso == "Entre 2 millones y 5 millones de pesos" ~ 3500000,
tingreso == "Más de 5 millones de pesos" ~ 5000000), #Paso 1
ingreso = if_else(is.na(ingreso), tingreso, ingreso))- Paso 3: Comparar el resultado de los tramos
movid_proc %>% select(ingreso, tingreso) %$%
print(dfSummary(., headings = FALSE, method = "render", varnumbers = F, lang = "es")) #Paso 3| Variable | Estadísticas / Valores | Frec. (% sobre válidos) | Gráfico | Válido | Perdidos |
|---|---|---|---|---|---|
| ingreso [numeric] |
Media (d-s) : 664667.4 (811775.8) min < mediana < max: 0 < 4e+05 < 1.2e+07 RI (CV) : 450000 (1.2) |
155 valores distintos | : : : : : . |
1151 (91.3%) |
110 (8.7%) |
| tingreso [numeric] |
Media (d-s) : 598198.6 (688242.3) min < mediana < max: 2e+05 < 425500 < 3500000 RI (CV) : 375500 (1.2) |
200000 : 47 (22.5%) 275000 : 57 (27.3%) 425500 : 38 (18.2%) 650500 : 35 (16.7%) 1000500 : 9 ( 4.3%) 1600500 : 15 ( 7.2%) 3500000 : 8 ( 3.8%) |
IIII IIIII III III I |
209 (16.6%) |
1052 (83.4%) |
Vemos que pasamos de tener 25,3% de datos perdidos en ingresos a un 8,72% (es decir, recuperamos un 16,58% de los casos). A ingresos se le pueden hacer tres transformaciones más
1. Logaritmizar: en caso de que queramos seguir trabajando ingresos como una variable continua es una buena opción.
2. Calcular el ingreso per cápita: si dividimos el ingreso por el tamaño del hogar (n° de habitantes en este), obtendremos el ingreso por persona.
3. Cálculo de medidas de posición acumulada: con los ingresos per cápita se puede calcular la media o mediana de medidas de posición acumulada como quitiles
movid_proc <- movid_proc %>%
mutate(log_ing = log(ingreso), #Log ingresos
ing_per = ingreso/tamanohogar, #Ingreso percapita
quintiles = dplyr::ntile(ing_per,
n = 5)) # n de categorias, para quintiles usamos 52.3 Dicotomizar variable dependiente
Es recurrente que en las encuestas sociales nos encontremos con preguntas con Escala Likert. Sin embargo, muchas veces estas no tienen una distribución normal, y más bien las respuestas están concentradas en algunas categorías de referencia.
Si bien no hay criterios canónicos para trabajar esas variables, tiene sentido indicar que más bien no representan un constructo con 5 o más niveles, sino que probablemente de 2. Re-especificar la variable como dicotómica no solo ayudará a trabajar de manera más realista el constructo, sino que facilitará las interpretaciones que queramos hacer de nuestro modelo.
Ocuparemos dos criterios para la dicotomización:
Medias: se ocupará como criterio discriminante la media de la variable (donde 1 puede ser los valores mayores a la media, y 0 los inferiores).
Mediana: la más frecuente en medidas ordinales como las escalas Likert es cuando el 50% de los casos se concentra en unas pocas categoría de respuesta (eg, “Muy de acuerdo” y “De acuerdo” serán 1 y el resto 0).
En el caso de la variable fatiga que indica “A medida que ha avanzado la crisis sanitaria, me siento cada vez más desmotivado para seguir las medidas de protección recomendadas”, recodificaremos a aquellos como 1 a quiénes asienten a esta frase (“Muy de acuerdo” y “De acuerdo”)
movid_proc <- movid_proc %>%
mutate(fatigadummy = case_when(fatiga %in% c(5,4) ~ 1,
fatiga %in% c(3,2,1) ~ 0, TRUE ~ NA_real_))2.4 Errores estándares robustos
En caso de que estemos ante problemas de heterocedasticidad debemos re-estimar nuestro modelo considerando errores estándares robustos
model_robust<- lmtest::coeftest(model1, vcov=sandwich::vcovHC(model1))2.5 Creación de índices
En el tutorial de dplyr ya habíamos abordado este punto. También está desarrollado de manera extensa en el práctico N°1. Por ello, solo lo cacularemos para aquellos ítems que mostraron posibilidad de ser colineales. Los pasos son
- Correlacionar para verificar que estamos ante la presencia de ítems que podrían estar midiendo un constructo común. Como vemos en la siguiente tabla, las correlaciones son altas
movid_proc %>% select(starts_with("c2")) %>%
mutate_all(~as.numeric(.)) %>%
sjPlot::tab_corr(., triangle = "lower")| c2_1 | c2_2 | c2_3 | c2_4 | |
|---|---|---|---|---|
| c2_1 | ||||
| c2_2 | 0.608*** | |||
| c2_3 | 0.599*** | 0.569*** | ||
| c2_4 | 0.483*** | 0.465*** | 0.586*** | |
| Computed correlation used pearson-method with listwise-deletion. | ||||
- Construcción de índice: este puede ser sumativo o promedio. Esto dependerá de la escala de los ítems y del sentido del constructo final que queremos utilizar. En nuestro caso crearemos una índice sumativa de
salud mental
movid_proc <- movid_proc %>%
mutate_at(vars(starts_with("c2")),~as.numeric(.)) %>%
rowwise() %>%
mutate(salud_mental = sum(c2_1,c2_2,c2_3,c2_4, na.rm = T))2.6 Eliminar casos influyentes
En caso de que estemos ante la prescencia de casos influyentes debemos seguir los siguientes pasos
n<- nobs(model1) #n de observaciones
k<- length(coef(model1)) # n de parametros
dcook<- 4/(n-k-1) #Punto de corte
# Datos donde se filtran los valores sobre el punto de corte
movid_proc_so <- broom::augment_columns(model1,data = movid_proc) %>% filter(.cooksd<dcook)Una vez finalizada las transformaciones calcular dos nuevos modelos
model1_fit <- lm(as.numeric(fatiga) ~ salud_mental +
trabaja + sexo + edad + ing_per,
data = movid_proc)
model2 <- lm(as.numeric(fatiga) ~ salud_mental +
trabaja + sexo + edad2 + ing_per,
data = movid_proc)
model3 <- glm(fatigadummy ~ salud_mental +
trabaja + sexo + edad2 + ing_per, family = "binomial",
data = movid_proc)Luego, podemos hacer un chequeo general de diagnósticos de robustez con check_model, pero ahora indicando que queremos evaluar todos los indicadores posibles
check_model(model1_fit, check = c("vif","normality", "linearity", "ncv", "homogeneity"))
check_model(model2, check = c("vif", "normality", "linearity", "ncv", "homogeneity"))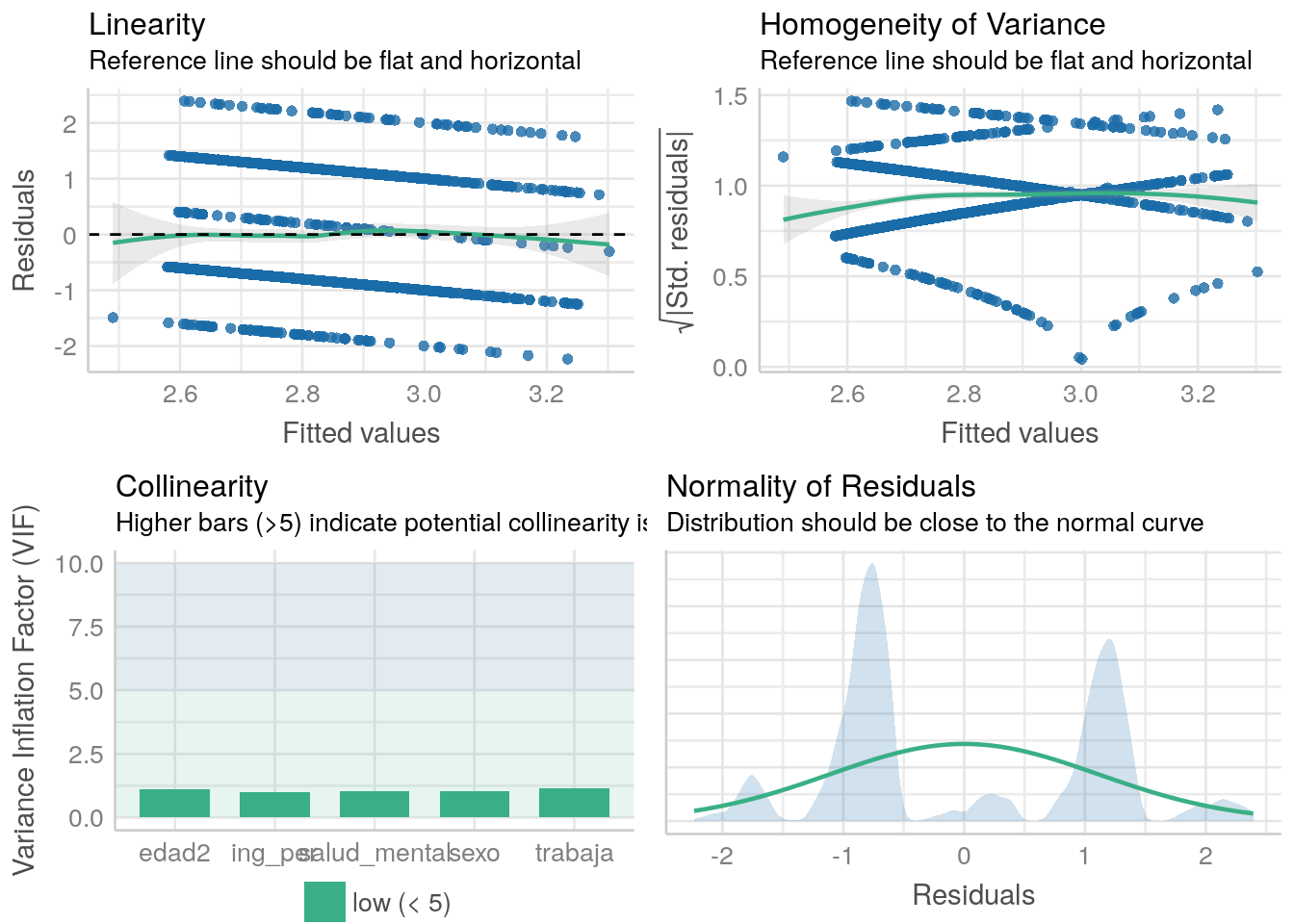
check_model(model3, check = c("vif", "homogeneity"))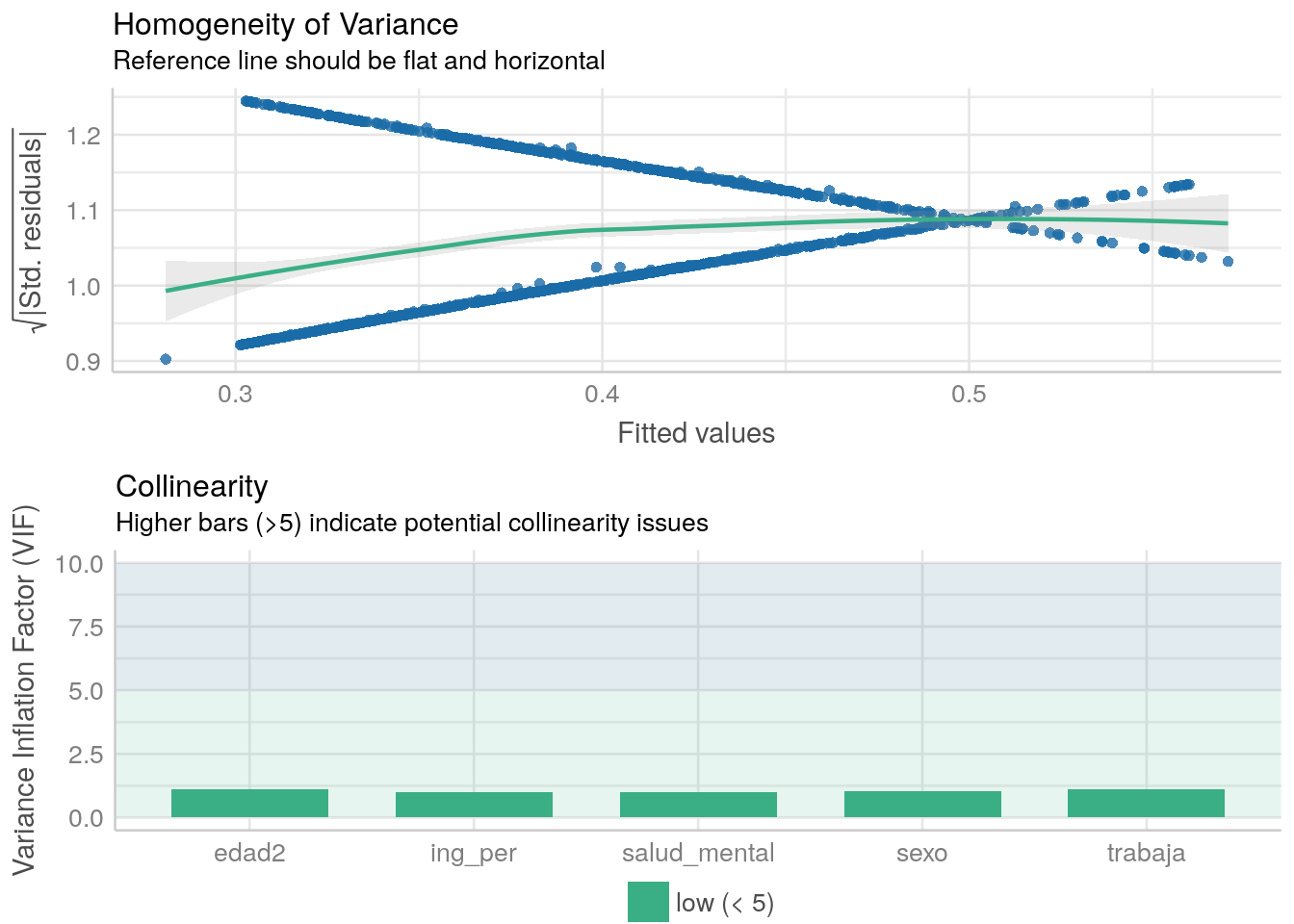
Existen otros diagnósticos posibles para abordar en nuestros modelos, todo con el propósito de mejorar la calidad de estos. Uno de ellos, y que no abordaremos por su extensión, es la ausencia de posibles interacciones entre las variables que no han sido modeladas (Fox & Weisberg 2018). En caso de su interés pueden revisar esto y ver su aplicación simple en R en el siguiente link.
3. Comparación
Tabla 3. Modelos de regresión que predice la fatiga a la pandemia| Modelo 1 | Modelo 2 | Modelo 3 | |
|---|---|---|---|
| (Intercept) | 2.60*** | 2.40*** | -1.09*** |
| (0.14) | (0.11) | (0.20) | |
| c2_1Varios días | -0.17 | ||
| (0.10) | |||
| c2_1Más de la mitad de los días | 0.23 | ||
| (0.16) | |||
| c2_1Casi todos los días | -0.08 | ||
| (0.14) | |||
| c2_2Varios días | -0.02 | ||
| (0.10) | |||
| c2_2Más de la mitad de los días | -0.07 | ||
| (0.17) | |||
| c2_2Casi todos los días | -0.10 | ||
| (0.15) | |||
| c2_3Varios días | 0.19 | ||
| (0.10) | |||
| c2_3Más de la mitad de los días | 0.23 | ||
| (0.17) | |||
| c2_3Casi todos los días | 0.29 | ||
| (0.16) | |||
| c2_4Varios días | 0.16 | ||
| (0.10) | |||
| c2_4Más de la mitad de los días | 0.24 | ||
| (0.17) | |||
| c2_4Casi todos los días | 0.32* | ||
| (0.16) | |||
| trabajaNo | 0.06 | 0.12 | 0.28* |
| (0.08) | (0.07) | (0.14) | |
| sexoMujer | 0.02 | 0.02 | 0.06 |
| (0.08) | (0.07) | (0.13) | |
| edad | 0.00 | ||
| (0.00) | |||
| ingreso | -0.00 | ||
| (0.00) | |||
| salud_mental | 0.04*** | 0.06** | |
| (0.01) | (0.02) | ||
| edad2 | 0.00 | 0.00 | |
| (0.00) | (0.00) | ||
| ing_per | 0.00 | 0.00 | |
| (0.00) | (0.00) | ||
| R2 | 0.04 | 0.02 | |
| Adj. R2 | 0.02 | 0.01 | |
| Num. obs. | 917 | 1128 | 1128 |
| AIC | 1510.51 | ||
| BIC | 1540.67 | ||
| Log Likelihood | -749.25 | ||
| Deviance | 1498.51 | ||
| p < 0.001; p < 0.01; p < 0.05 | |||
Si bien en con la tabla N°3 podemos tener un panorama, es imprescindible recordar que para comparar modelos (en su robustez y ajuste) es necesario que estos tengan (1) la misma variable de respuesta y (2) el mismo número de observaciones.
compare_performance(model1_fit, model2) %>%
print_md()| Name | Model | AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma |
|---|---|---|---|---|---|---|---|
| model1_fit | lm | 3452.28 | 3487.48 | 0.02 | 0.01 | 1.11 | 1.11 |
| model2 | lm | 3452.24 | 3487.44 | 0.02 | 0.01 | 1.11 | 1.11 |
plot(compare_performance(model1_fit, model2))
Ahora bien, esto no quita que, considerando que el ajuste entre el model1_fit y el modelo2 no cambia sustantivamente, consideremos en seleccionar el modelo3 por criterios más sustantivos. Podemos asegurarnos de esta comparación entre el modelo1 y modelo2 con un test que permite facilitar la decisión sobre la significancia de los índices que estamos viendo
test_performance(model1_fit, model2) %>%
print_md()| Name | Model | log_BF | BF |
|---|---|---|---|
| model1_fit | lm | 0.00 | |
| model2 | lm | 0.02 |
Each model is compared to model1_fit.
Referencias
Lüdecke, Makowski, Waggoner & Patil (2020). Assessment of Regression Models Performance. CRAN. Available from https://easystats.github.io/performance/
Lüdecke, Makowski, Waggoner & Patil (2021). performance: Assessment of Regression Models Performance. Journal of Open Source Software. 60(6). pp.3139. doi: 10.21105/joss.03139
Fox J, Weisberg S. Visualizing Fit and Lack of Fit in Complex Regression Models with Predictor Effect Plots and Partial Residuals. Journal of Statistical Software 2018;87. https://www.jstatsoft.org/article/view/v087i09