Práctica 9: Regresión Logística 2
Índice
Objetivo
La siguiente práctica tiene el objetivo de introducir a los estudiantes en los modelos de regresión logística multivariada. Al igual que en la práctica anterior emplearemos una variable dependiente dicotómica, de modo tal que veremos de qué una serie de variables independientes nos permiten predecir la ocurrencia de un determinado evento. Para ello, utilizaremos la base de datos de la Encuesta sobre Conflicto y Cohesion Social en Chile 2014 para analizar los determinantes de la participación en las elecciones del año 2013.
Librerías
pacman::p_load(dplyr, summarytools, ggmosaic, sjPlot, texreg)Datos
La Encuesta sobre Conflicto y Cohesión Social en Chile (ENACOES 2014) es el primer estudio de este tipo que busca mapear los conflictos y la cohesión en el país. Su objetivo fundamental es aportar a la comprensión de las creencias, actitudes y percepciones de los chilenos hacia las distintas dimensiones de la convivencia y el conflicto. La población objetivo son hombres y mujeres entre 15 y 75 años de edad con un alcance nacional, donde se obtuvo una muestra final de 2025 casos. Para el caso de este ejercicio, se trabajará con una submuestra de 1974 individuos que estuvieron habilitados para votar en el año 2013.
#Cargamos la base de datos desde internet
load(url("https://multivariada.netlify.com/assignment/data/enacoes.RData"))Explorar datos
A partir de la siguiente tabla se obtienen estadísticos descriptivos que luego serán relevantes para la interpretación de nuestros modelos.
view(dfSummary(enacoes, headings = FALSE, method = "render"))| No | Variable | Label | Stats / Values | Freqs (% of Valid) | Graph | Valid | Missing | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | voto [factor] | Votó en última elección | 1. 0 2. 1 |
|
1974 (100.0%) | 0 (0.0%) | |||||||||||||||||||||
| 2 | sexo [factor] | Sexo entrevistado | 1. 0 2. 1 |
|
1974 (100.0%) | 0 (0.0%) | |||||||||||||||||||||
| 3 | edad [numeric] | Edad entrevistado | Mean (sd) : 45.1 (16) min < med < max: 18 < 45 < 75 IQR (CV) : 26 (0.4) | 58 distinct values | 1974 (100.0%) | 0 (0.0%) | |||||||||||||||||||||
| 4 | educ [factor] | Nivel Educacional | 1. 1 2. 2 3. 3 4. 4 5. 5 |
|
1974 (100.0%) | 0 (0.0%) |
Generated by summarytools 0.9.9 (R version 4.0.3)
2021-06-29
Lo primero que debemos observar es la distribución de la participación electoral, donde 0 son quienes nos votaron en la última elección y 1 los que sí lo hicieron. En este caso, vemos que un 67,1% (1325) señaló haber participado en la última elección, en contraste de un 32,9% que no lo hizo. En este sentido, vemos que existen aproximadamente 2/3 de los individuos de la muestra que sí acudieron a votar, por tanto ahora vamos a revisar cómo se distribuyen estas respuestas según el sexo y el nivel educacional de el entrevistado.
En primera instancia nos centraremos en las variables sexo y voto. Como podemos notar la categoría de respuesta de estas variables son 0 y 1, es decir, estamos ante variables dicotómicas.
En segunda instancia, observaremos la distribución de participación electoral según el Nivel educacional (educ), la cual en este caso hemos recodificado en cinco niveles educacionales.
Con la función tab_xtab del paquete sjPlot podemos realizar una tabla de contingencia donde se señala la proporción de la participación electoral según sexo.
tab_xtab(var.row = enacoes$voto,enacoes$sexo,show.cell.prc = T,show.summary = F)|
Votó en última elección |
Sexo entrevistado | Total | |
|---|---|---|---|
| Hombre | Mujer | ||
| No votó |
254 12.9 % |
395 20 % |
649 32.9 % |
| Votó |
549 27.8 % |
776 39.3 % |
1325 67.1 % |
| Total |
803 40.7 % |
1171 59.3 % |
1974 100 % |
Teniendo en cuenta que existen 2/3 (67,1%) de las personas en Chile que han declarado haber votado en la última elección, la tabla anterior nos muestra que del total de personas que votan, las participación electoral es mayor en las mujeres, lo cual equivale a un 39,3% del total en desmedro del 27,8% que representado por los hombres.
tab_xtab(var.row = enacoes$voto,enacoes$educ,
show.cell.prc = T,show.summary = F, encoding = " ")|
Votó en última elección |
Nivel Educacional | Total | ||||
|---|---|---|---|---|---|---|
|
Primaria incompleta o menos |
Primaria | Secundaria | Técnica Superior |
Universitaria o postgrado |
||
| No votó |
55 2.8 % |
47 2.4 % |
320 16.2 % |
182 9.2 % |
45 2.3 % |
649 32.9 % |
| Votó |
124 6.3 % |
120 6.1 % |
558 28.3 % |
331 16.8 % |
192 9.7 % |
1325 67.2 % |
| Total |
179 9.1 % |
167 8.5 % |
878 44.5 % |
513 26 % |
237 12 % |
1974 100 % |
Adicionalmente, la tabla anterior nos muestra la distribución de la participación electoral según cinco categorías de nivel educacional. Como podemos observar, la participación electoral se concentra en los niveles educacionales secundario con un 28,3% y superior técnica y universitaria, con un 16,8% y 9,7% respectivamente. Por otro lado, podemos observar una baja participación electoral de los grupos con nivel educacional más bajo, donde las personas con Primaria incompleta o menos representan un 6,3% y aquellas con Primaria completa son el 6,1%.
Al igual que la práctica anterior, podemos representar gráficamente estas distribuciones a través del paquete ggmosaic que con su función geom_mosaic. A continuación se presentan dos gráficos para la participación electoral según sexo y nivel educacional.
ggplot(enacoes) +
geom_mosaic(aes(x=product(voto, sexo), fill=sexo)) +
geom_label(data = layer_data(last_plot(), 1),
aes(x = (xmin + xmax)/ 2,
y = (ymin + ymax)/ 2,
label = paste0(round((.wt/sum(.wt))*100,1),"%"))) +
labs(y = "Voto última elección",
x = "Sexo") +
scale_fill_discrete(name = "",
labels = c("Hombre","Mujer"))+
scale_y_continuous(breaks = c(0,1),
labels = c("No votó","Votó")) +
theme(legend.position="bottom")
ggplot(enacoes) +
geom_mosaic(aes(x=product(voto, educ), fill=educ)) +
geom_label(data = layer_data(last_plot(), 1),
aes(x = (xmin + xmax)/2,
y = (ymin + ymax)/2,
label = paste0(round((.wt/sum(.wt))*100,1),"%"))) +
labs(y = "Voto última elección",
x = "Nivel Educacional") +
scale_fill_discrete(name = "",
labels = c("Primaria incompleta o menos",
"Primaria",
"Secundaria", "Técnica o Superior",
"Universitaria o postgrado"))+
scale_y_continuous(breaks = c(0,1),labels = c("No votó","Votó")) +
theme(legend.position="bottom")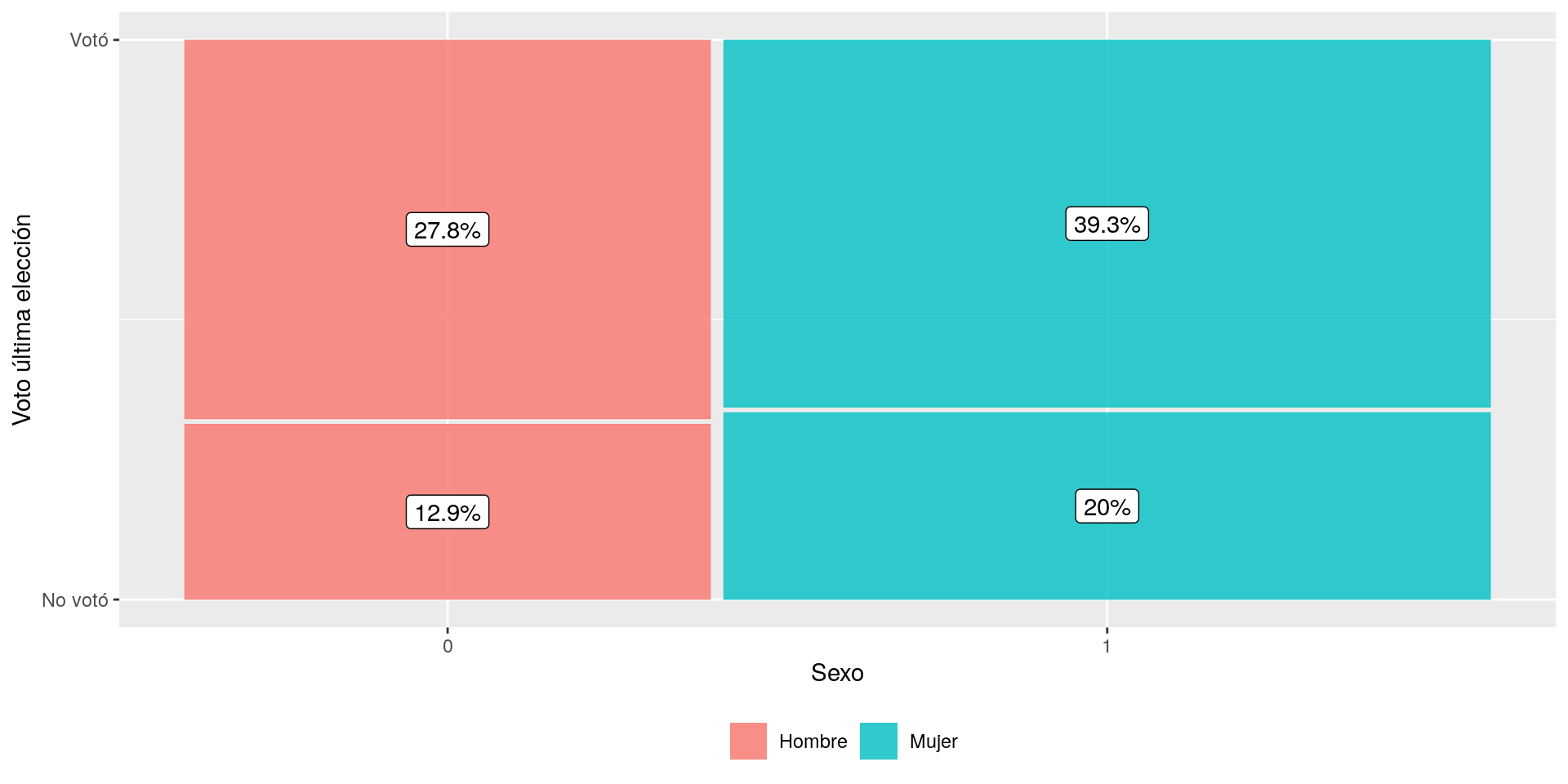
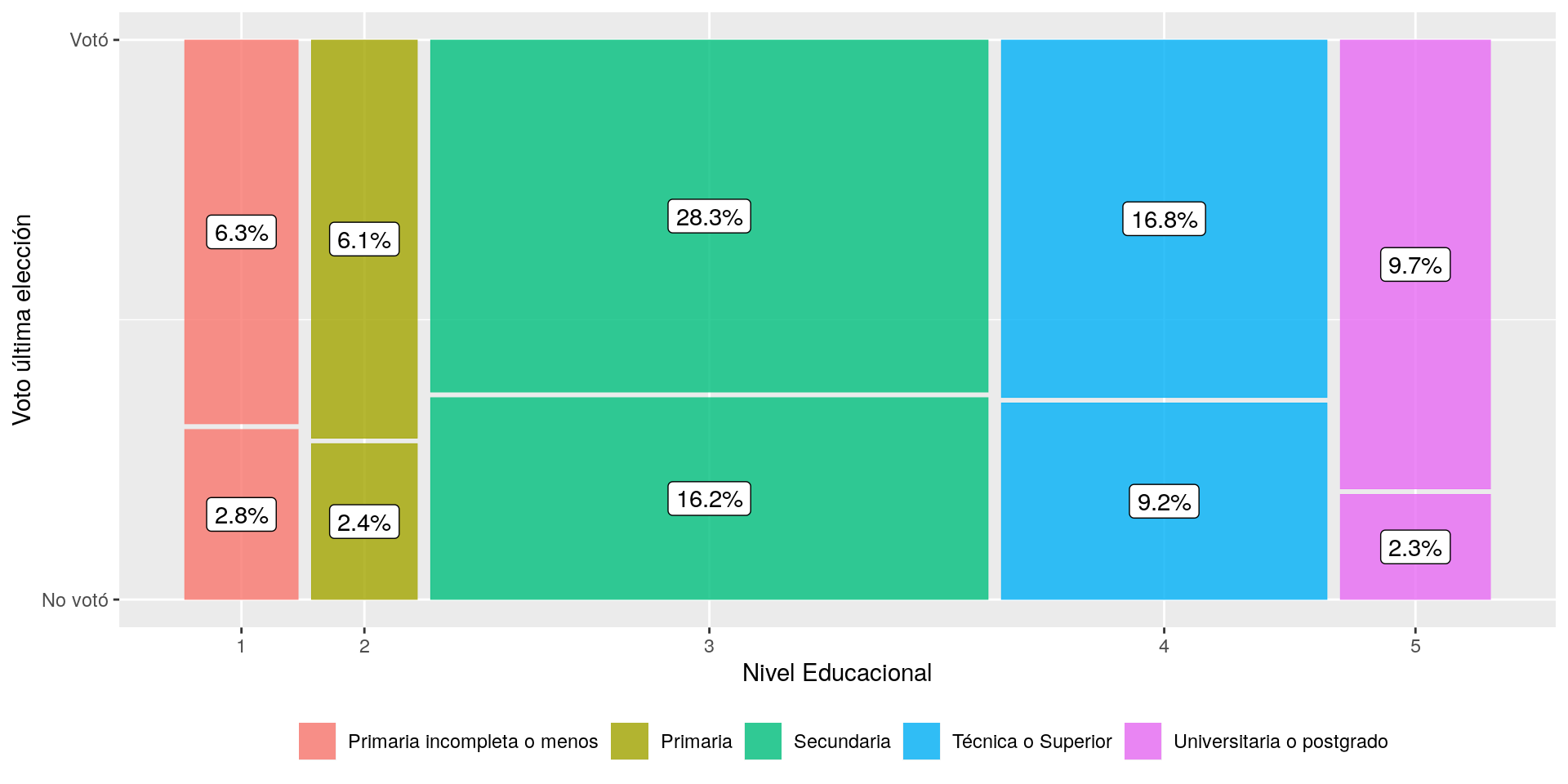
Figure 1: Participación electoral en 2013 según Sexo y Nivel Educacional
Estimación
La función pincipal para la estimación de modelos de regresión logística es glm(), especificando el argumento family="binomial", lo cual le indica a la función que estamos prediciendo una variable binaria. Al igual que con lm(), debemos especificar los predictores y la base de datos a emplear. A continuación, estimaremos una serie de modelos de regresión logística que nos permitan determinar de qué manera el sexo, la edad y el nivel educacional de las personas pueden predecir la participación electoral.
m00 <- glm(voto~1,data = enacoes,family = "binomial")
m01 <- glm(voto~sexo,data = enacoes,family = "binomial")
m02 <- glm(voto~edad,data = enacoes,family = "binomial")
m03 <- glm(voto~sexo+edad+educ,data = enacoes,family = "binomial")Presentación de resultados
Para construir una tabla de regresión podemos usar la librería texreg:
Esto se puede hacer si se utiliza RMarkdown (no es requisito en este curso, para los interesad_s pueden revisar material del curso ciencia social abierta )
Instalar librería texreg. Si bien existe una versión en CRAN, no nos permite usar el argumento
custom.gof.rowspara agregar estadísticos de ajuste adicionales, así que para instalar:remotes::install_github("leifeld/texreg")Existen tres variaciones para crear tablas:
screenreg(): nos muestra la tabla en la consola de Rhtmlreg(): produce una tabla en formato html (como las que vemos en este documento)texreg(): produce una tabla en formato
Para que el resultado pueda ser
renderizadodesde un documento RMarkdown a pdf o html, debe estar en un chunk con las siguientes especificaciones:
```{r results='asis', echo=FALSE}
htmlreg(list(m01,m02,m03))
```- Para personalizar nuestra tabla podemos ir agregando más información, tales como los nombres de los coeficientes o el nombre de los modelos:
```{r results='asis', echo=FALSE}
htmlreg(l = list(m00,m01,m02,m03),
custom.coef.names=c("Intercepto","Sexo (Mujer=1)","Edad","Primaria","Secundaria", "Técnica o Superior","Universitaria o postgrado"),
custom.model.names = c("Modelo 0","Modelo 1","Modelo 2", "Modelo 3"))
```Tabla de regresión
| Modelo 0 | Modelo 1 | Modelo 2 | Modelo 3 | |
|---|---|---|---|---|
| Intercepto | 0.71*** | 0.77*** | -1.07*** | -2.04*** |
| (0.05) | (0.08) | (0.15) | (0.29) | |
| Sexo (Mujer=1) | -0.10 | -0.02 | ||
| (0.10) | (0.10) | |||
| Edad | 0.04*** | 0.05*** | ||
| (0.00) | (0.00) | |||
| Primaria | 0.34 | |||
| (0.25) | ||||
| Secundaria | 0.47* | |||
| (0.19) | ||||
| Técnica o Superior | 0.88*** | |||
| (0.22) | ||||
| Universitaria o postgrado | 1.53*** | |||
| (0.25) | ||||
| AIC | 2502.30 | 2503.34 | 2334.32 | 2290.54 |
| Log Likelihood | -1250.15 | -1249.67 | -1165.16 | -1138.27 |
| Deviance | 2500.30 | 2499.34 | 2330.32 | 2276.54 |
| Num. obs. | 1974 | 1974 | 1974 | 1974 |
|
Errores estándar entre paréntesis |
||||
En la tabla anterior podemos observar cuatro modelos distintos:
| Modelo | Predictores |
|---|---|
| Modelo 0 | modelo nulo (sin predictores) |
| Modelo 1 | Incluye sexo |
| Modelo 2 | Incluye edad |
| Modelo 3 | Incluye sexo, edad y nivel educacional |
Regresión logística sin predictores
El modelo sin predictores nos permite conocer la probabilidad de votar. En este caso, vemos que se obtiene un intercepto de 0.71 correspondiente a
knitr::kable(sjmisc::frq(enacoes$voto,show.na = F, title = F))
|
Entonces, tenemos que p = exp(0.71)/(1 + exp(0.71))= 0.67.
Regresión logistica con variable binaria como predictor
El modelo con un predictor binario como sexo nos permite estimar la probabilidad de votar para las mujeres (sexo = 1), respecto a los hombres (sexo = 0). En este caso, los resultados muestran el valor del intercepto (0.77) y para sexo (-0.10). Antes de interpretar, demos una mirada a la distribución de la participación electoral según sexo:
## sexo Hombre Mujer
## voto
## No votó 254 395
## Votó 549 776En nuestros datos, ¿cuáles son las chances (odds) de votar para los hombres y para las mujeres? Con la información de la tabla de contingencia podemos realizar los cálculos manualmente: para los hombres (sexo = 0), las odds de votar son (549/803)/(254/803) = 0.683 /0.316 = 2.16. A su vez, para las mujeres, las odds de votar son (776/1171)/(395/1171) = 0.662/0.337 = 1.96. Entonces, las odds ratio para las mujeres respecto de los hombres es (776/395)/(549/254) = (776x254)/(549x395) = 0.907. Por tanto, por cada hombre que vota, votan 0,9 mujeres, o por cada 10 hombres que votan, votan 9 mujeres.
Ahora, si observamos los resultados de la tabla de regresión vemos que el intercepto es 0.77, el cual representa las log-odds para los hombres en tanto corresponde a la categoría de referencia (sexo = 0). Usando las odds de votar para los hombres calculada en el apartado anterior, podemos confirmarlo: log(2.16) = 0.77. A su vez, el log-odds para las mujeres corresponde al log del odds-ratio de las odds de las mujeres y de los hombres calculado anteriormente: log(0.907) = -0.10. El output tradicional de R cuando usamos glm() nos entrega los coeficientes en unidades de log-odds, por tanto es necesario realizar la exponenciación de dichos coeficientes para realizar la interpretación en unidades de odds-ratio.
Regresión logística con variable continua como predictor
Ahora, estimaremos un modelo empleando la edad como predictor continuo. En este caso, el intercepto corresponde a los log-odds de una persona con “edad 0”. En otras palabras, las odds de votar cuando se tiene edad 0 es exp(-1.07) = 0.343. Lo importante es que si observamos la distribución de la variable edad, vemos que el valor mínimo es 18 años, por tanto, sabemos que este coeficiente no posee una interpretación sustantiva directamente. Lo más relevante es que el intercepto en ese modelo corresponde a los log-odds de votar en el hipotético caso de tener edad cero.
Entonces, ¿cómo interpretamos el coeficiente de edad?. Para esto, lo ideal es tener en cuenta todos los valores de la ecuación:
Una manera de hacerlo es fijar edad en algún valor, por ejemplo un sujeto de con 54 años. Entonces, el valor del log-odds para una persona con 54 años es:
Ahora, el valor de los log-odds para una persona con 55 años es:
Entonces, podemos decir que el coeficiente para edad es la diferencia en el log-odds. En otras palabras, por una unidad de incremento en edad (1 año), el cambio esperado en los log-odds es de 0.04.
Ahora, ¿cómo traducimos este cambio en odds?. Tenemos que:
Finalmente, podemos decir que por el incremento de una unidad en edad (1 año), se espera ver un incremento aproximado de un 4% en las odds de ir a votar. Este porcentaje no depende de los valores en los cuales se mantenga edad.
Regresión logística con múltiples predictores
Este ejemplo representa el modelo multivariado para participación electoral. Cada coeficiente prepresenta el cambio predicho en el log-odds de votar por un incremento/cambio en la variable, manteniendo todas las demás variables constantes. Cada coeficiente exponenciado (exp), representa el ratio de dos odds (por ejemplo, mujer respecto a hombre), o el cambio en las odds por el incremento de una unidad de la variable independiente (por ejemplo, un año de edad), manteniendo las demás variables constantes.
Entonces, si observamos el coeficiente de sexo en el Modelo 3, vemos que el odds-ratio de las mujeres sobre los hombres es de exp(-0.02)= 0.98, es decir que las odds de votar en las elecciones son 1,9% (exp(-0.02)-1 = 0.98-1) más bajas para las mujeres respecto a los hombres, manteniendo edad y el nivel educacional constante.
La variable nivel educacional posee 5 niveles, donde “Primaria incompleta o menos” es la categoría de referencia, por tanto, los coeficientes se deben interpretar respecto dicha categoría. Por ejemplo, tenemos que el odds-ratio para Primaria es de exp(0.34) = 1.40, por lo tanto las odds de votar en las elecciones son 40% (exp(-0.02)-1 = 1.40-1) más altas para las personas que completaron la educación primaria respecto a quienes tienen educación primaria incompleta o menos, manteniendo sexo y edad en valores constantes.
Ahora, observando el log-odds para las personas son educación Universitaria o postgrado podemos calcular que el odds-ratio para esta categoría es de exp(1.53) = 4.61, lo cual nos indica que las odds de votar son 361% exp(1.53)-1 = 4.61-1 más altas para las personas con educación universitaria o postgrado respecto a quienes tienen educación primaria incompleta o menos, manteniendo sexo y edad en valores constantes.
Otra alternativa de interpretación es a través del cálculo de las probabilidades predichas. Por ejemplo ¿cuál es la probabilidad de votar según los distintos niveles educacionales manteniendo constante sexo y edad?. En este caso usaremos una persona hipotética que es mujer (sexo=1) de 55 años.
Tenemos nuestros coeficientes para el Modelo 3:
m03$coefficients## (Intercept) sexo1 edad educ2 educ3 educ4
## -2.03578412 -0.02351809 0.04911213 0.33653007 0.46911435 0.88442909
## educ5
## 1.52605507Calculamos las log-odds para cada caso:
# Intercept sexo*1 edad*55 educ2 educ3 educ4 educ5
ed01<- -2.03578412+(-0.0235*1)+(0.0491*55)+(0.3365*0)+(0.4691*0)+(0.8844*0)+(1.5260*0) # mujer 55 anios Primaria incompleta
ed02<- -2.03578412+(-0.0235*1)+(0.0491*55)+(0.3365*1)+(0.4691*0)+(0.8844*0)+(1.5260*0) # mujer 55 anios Primaria
ed03<- -2.03578412+(-0.0235*1)+(0.0491*55)+(0.3365*0)+(0.4691*1)+(0.8844*0)+(1.5260*0) # mujer 55 anios Secundaria
ed04<- -2.03578412+(-0.0235*1)+(0.0491*55)+(0.3365*0)+(0.4691*0)+(0.8844*1)+(1.5260*0) # mujer 55 anios Tecnica
ed05<- -2.03578412+(-0.0235*1)+(0.0491*55)+(0.3365*0)+(0.4691*0)+(0.8844*0)+(1.5260*1) # mujer 55 anios UniversitariaCalculamos las probabilidades predichas de la siguiente manera:
pr.ed01<- exp(ed01)/(1+exp(ed01))
pr.ed02<- exp(ed02)/(1+exp(ed02))
pr.ed03<- exp(ed03)/(1+exp(ed03))
pr.ed04<- exp(ed04)/(1+exp(ed04))
pr.ed05<- exp(ed05)/(1+exp(ed05))Finalmente, se presenta la tabla resumen a continuación:
as.data.frame(rbind(c(ed01,exp(ed01),pr.ed01),
c(ed02,exp(ed02),pr.ed02),
c(ed03,exp(ed03),pr.ed03),
c(ed04,exp(ed04),pr.ed04),
c(ed05,exp(ed05),pr.ed05))) %>%
rename("log-odds"=V1,
"exp(log-odds)"=V2,
"exp(odds)/(1-exp(odds)" =V3) %>%
mutate("Nivel educacional"=c("Primaria incompleta o menos","Primaria","Secundaria","Técnica","Univsersitaria")) %>%
select("Nivel educacional", everything()) %>%
knitr::kable(digits = 3, row.names = F)| Nivel educacional | log-odds | exp(log-odds) | exp(odds)/(1-exp(odds) |
|---|---|---|---|
| Primaria incompleta o menos | 0.641 | 1.899 | 0.655 |
| Primaria | 0.978 | 2.658 | 0.727 |
| Secundaria | 1.110 | 3.035 | 0.752 |
| Técnica | 1.526 | 4.598 | 0.821 |
| Univsersitaria | 2.167 | 8.734 | 0.897 |
La librería sjPlot posee la función plot_model() la cual, dentro de otras cosas, nos permite visualizar las probabilidades predichas para un modelo de regresión logística.
plot_model(m03,type = "pred",
terms = "educ",
title = "Probabilidades predichas para Voto según nivel educacional") + geom_line()
En conjunto, podemos observar que en la medida que aumenta el nivel educacional de las personas, la probabilidad de que participen en las elecciones tiende a ser mayor, manteniendo edad y sexo constante.
Medidas de Ajuste
El ajuste de los modelos de regresión logística puede ser evaluado de distintas maneras. Generalmente se realiza a través del contraste con otros modelos con más o menos predictores, lo cual nos permite elegir entre las mejores especificaciones. Adicionalmente, presentaremos la manera de incorporar estas medidas de ajuste a la tabla de regresión del apartado anterior.
En este ejercicio emplearemos (1) Test de Devianza y (2) Pseudo-R2 de McFadden.
Test de razón de verosimilitud / diferencia de devianza
Este test nos permite comparar las verosimilitudes del modelo con predictores, respecto a un modelo con menos predictores. En este caso, emplearemos la función anova() el cual realiza un test basado en la distribución chi-cuadrado donde se contrasta el modelo en cuestión respecto a un modelo sin predictores (modelo “nulo”).
En nuestro caso, comparamos nuestro modelo sin predictores con los posteriores modelos para sexo, edad y nivel educacional.
test01<- anova(m00,m01,test = "Chisq")
test02<- anova(m00,m02,test = "Chisq")
test03<- anova(m00,m03,test = "Chisq")
lrt01<- rbind(test01,test02,test03) %>% unique()
row.names(lrt01) <- c("Modelo nulo",
"Modelo 1",
"Modelo 2",
"Modelo 3")
knitr::kable(lrt01,digits = 3, caption = "Test de devianza entre modelos")| Resid. Df | Resid. Dev | Df | Deviance | Pr(>Chi) | |
|---|---|---|---|---|---|
| Modelo nulo | 1973 | 2500.296 | |||
| Modelo 1 | 1972 | 2499.342 | 1 | 0.954 | 0.329 |
| Modelo 2 | 1972 | 2330.325 | 1 | 169.971 | 0.000 |
| Modelo 3 | 1967 | 2276.545 | 6 | 223.751 | 0.000 |
Modelo nulo vs. Modelo 1: La diferencia entre los modelos no es estadísticamente significativa con una probabilidad
Modelo nulo vs. Modelo 2: La diferencia entre los modelos es estadísticamente significativa con una probabilidad
Modelo nulo vs. Modelo 3: La diferencia entre los modelos es estadísticamente significativa con una probabilidad
Podemos guardar los valores
test.pvalues1<- test01$`Pr(>Chi)`[2]
test.pvalues2<- test02$`Pr(>Chi)`[2]
test.pvalues3<- test03$`Pr(>Chi)`[2]Pseudo-R2 de McFadden
Esta medida de ajuste nos entrega una magnitud comparativa entre el modelo con predictores y el modelo nulo (sin predictores). Este se basda en los valores del loglikelihood de cada modelo.
- LL es el log likelihood del modelo
- LM es el modelo posterior (con predictores)
- L0 es el modelo nulo
Podemos calcularlos manualmente de la siguiente manera:
1-(logLik(m01)[1]/ logLik(m00)[1]) # modelo 1 vs modelo nulo
1-(logLik(m02)[1]/ logLik(m00)[1]) # modelo 2 vs modelo nulo
1-(logLik(m03)[1]/ logLik(m00)[1]) # modelo 3 vs modelo nulo## [1] 0.0003817169
## [1] 0.06798047
## [1] 0.08948998También, podemos utilizar la función PseudoR2() de la librería DescTools. A continuación los calculamos y guardamos para incluirlos en la tabla de regresión.
mfr2.00 <- DescTools::PseudoR2(m00)
mfr2.01 <- DescTools::PseudoR2(m01)
mfr2.02 <- DescTools::PseudoR2(m02)
mfr2.03 <- DescTools::PseudoR2(m03)r2<- as.data.frame(cbind(c(mfr2.00,mfr2.01,mfr2.02,mfr2.03)))
rownames(r2) <- c("Modelo nulo",
"Modelo 1",
"Modelo 2",
"Modelo 3")
knitr::kable(r2,digits = 3, col.names = c("McFadden R2"))| McFadden R2 | |
|---|---|
| Modelo nulo | 0.000 |
| Modelo 1 | 0.000 |
| Modelo 2 | 0.068 |
| Modelo 3 | 0.089 |
De esta manera, podemos observar que el cálculo del Pseudo R2 nos indica que el Modelo 1 no aporta mayor a la predicción, en contraste con el Modelo 2 y 3.
Presentación de resultados
Existen distintas librerías para presentar modelos de regresión, tales como las funciones tab_modeñ() o stargazer() que ya hemos revisado anteriormente. En este caso vamos a usar htmlreg() de la librería texreg. Por defecto, la función nos entrega la siguiente salida:
htmlreg(l = list(m03,m03), doctype = FALSE)| Model 1 | Model 2 | |
|---|---|---|
| (Intercept) | -2.04*** | -2.04*** |
| (0.29) | (0.29) | |
| sexo1 | -0.02 | -0.02 |
| (0.10) | (0.10) | |
| edad | 0.05*** | 0.05*** |
| (0.00) | (0.00) | |
| educ2 | 0.34 | 0.34 |
| (0.25) | (0.25) | |
| educ3 | 0.47* | 0.47* |
| (0.19) | (0.19) | |
| educ4 | 0.88*** | 0.88*** |
| (0.22) | (0.22) | |
| educ5 | 1.53*** | 1.53*** |
| (0.25) | (0.25) | |
| AIC | 2290.54 | 2290.54 |
| BIC | 2329.66 | 2329.66 |
| Log Likelihood | -1138.27 | -1138.27 |
| Deviance | 2276.54 | 2276.54 |
| Num. obs. | 1974 | 1974 |
| p < 0.001; p < 0.01; p < 0.05 | ||
Dentro de la misma función, existen más opciones para personalizar el reporte, incluyendo el argumento custom.gof.rows señalado en el apartado anterior, el cual emplearemos para incluirlos resultados delTest de Devianza y el Pseudo R2. En este caso, incluiremos una versión con coeficientes en log-odds del Modelo 3 y su posterior transformación a odds-ratio (OR), además de remplazar los errores estándar por intervalos de confianza.
Para transformar los coeficientes de log-odds a odds-ratio realizamos lo siguiente:
or <- texreg::extract(m03)
or@coef <- exp(or@coef)htmlreg(l = list(m03,or), doctype = F,caption = "",caption.above = T,
custom.model.names = c("Modelo 3", "Modelo 3 (OR)"),
custom.coef.names = coef.labs,
ci.force = c(TRUE,TRUE),
override.coef = list(coef(m03),or@coef),
custom.gof.rows=list("Deviance Test ($p$)" = c(test.pvalues3,
test.pvalues3),
"Pseudo R2" = c(mfr2.03,mfr2.03)),
custom.note = "$^{***}$ p < 0.001; $^{**}$ p < 0.01; $^{*}$ p < 0.05 <br> Errores estándar entre paréntesis. <br> **Nota**: La significancia estadística de los coeficientes en unidades de Odds ratio está calculada en base a los valores $t$, <br> los cuales a su vez se calculan en base a $log(Odds)/SE$")| Modelo 3 | Modelo 3 (OR) | |
|---|---|---|
| Intercepto | -2.04* | 0.13 |
| [-2.60; -1.47] | [-0.43; 0.70] | |
| Sexo (Mujer=1) | -0.02 | 0.98* |
| [-0.23; 0.18] | [ 0.77; 1.18] | |
| Edad | 0.05* | 1.05* |
| [ 0.04; 0.06] | [ 1.04; 1.06] | |
| Primaria | 0.34 | 1.40* |
| [-0.15; 0.82] | [ 0.91; 1.89] | |
| Secundaria | 0.47* | 1.60* |
| [ 0.09; 0.85] | [ 1.22; 1.98] | |
| Técnica o Superior | 0.88* | 2.42* |
| [ 0.46; 1.31] | [ 2.00; 2.84] | |
| Universitaria o postgrado | 1.53* | 4.60* |
| [ 1.03; 2.02] | [ 4.11; 5.09] | |
|
Deviance Test ( |
0.00 | 0.00 |
| Pseudo R2 | 0.09 | 0.09 |
| AIC | 2290.54 | 2290.54 |
| BIC | 2329.66 | 2329.66 |
| Log Likelihood | -1138.27 | -1138.27 |
| Deviance | 2276.54 | 2276.54 |
| Num. obs. | 1974 | 1974 |
|
Errores estándar entre paréntesis. Nota: La significancia estadística de los coeficientes en unidades de Odds ratio está calculada en base a los valores los cuales a su vez se calculan en base a |
||
Una alternativa a las tablas de regresión son los coefplots. Como hemos visto en prácticas anteriores, este tipo de gráficos muestran el valor de coeficiente acompañados de sus intervalos de confianza. En este caso, vemos que la función plot_model nos entrega por defecto los coeficientes en unidades de odds-ratio, por tanto el valor 1 representa el límite para la significancia estadística, a diferencia del 0 cuando se encuentra en unidades de log-odds. En este caso, conforme a lo presentado en la tabla de regresión, el coeficiente de Edad y Educación Secundaria, Técnica superior y Universitaria poseen intervalos de confianza que no contienen el valor 1, por tanto son estadísticamente signficativos.
plot02<- plot_model(m03,vline.color = "grey")
plot01<- plot_model(m03,vline.color = "grey",transform = NULL)
plot_grid(list(plot02,plot01),tags = c(" "," "),
margin = c(0,0,0,0))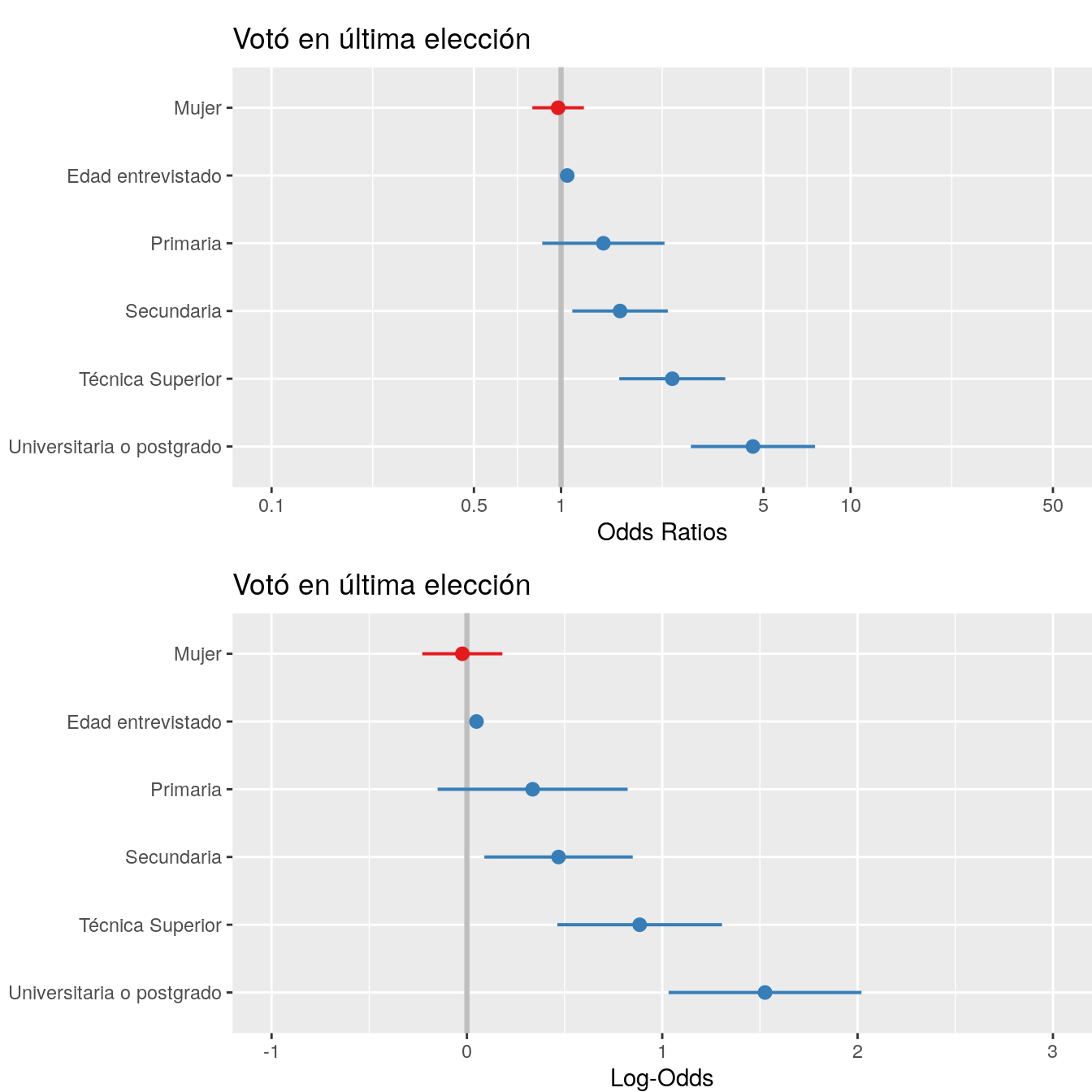
Figure 2: Modelo de regresión con y sin exponenciar (exp)
Video tutorial
Reporte de progreso
Contestar aquí.