Práctica 8. Regresión Logística 1
Índice
Objetivo
La siguiente práctica tiene el objetivo de introducir a los estudiantes en los modelos de regresión logística, que permite la estimación con una variable dependiente categórica dicotómica. En esta primera parte nos centraremos en conceptos centrales para estos modelos, que son probabilidades, chances (odds) y razón de chances (odds-ratio).
Librerías
pacman::p_load(dplyr, summarytools, ggmosaic, finalfit)Datos
El Titanic fue un transatlántico británico, el mayor barco del mundo al finalizar su construcción, que se hundió en la madrugada del 15 de abril de 1912 durante su viaje inaugural desde Southampton a Nueva York. En el hundimiento del Titanic murieron 619 personas de las 1046 que iban a bordo, lo que convierte a esta tragedia en uno de los mayores naufragios de la historia ocurridos en tiempo de paz. Con esta base realizaremos una serie de ejercicios para determinar la probabilidad de sobrevivir en base al sexo de los tripulantes.
#Cargamos la base de datos desde internet
load(url("https://multivariada.netlify.com/assignment/data/titanic.RData"))Explorar datos
A partir de la siguiente tabla se obtienen estadísticos descriptivos que luego serán relevantes para la interpretación de nuestros modelos.
view(dfSummary(tt, headings = FALSE, method = "render"))| No | Variable | Stats / Values | Freqs (% of Valid) | Graph | Valid | Missing | ||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | pclass [factor] | 1. Clase Alta 2. Clase Intermedia 3. Clase Baja |
|
1046 (100.0%) | 0 (0.0%) | |||||||||||||||||||||||||||||||||||||||||||
| 2 | survived [factor] | 1. No sobrevive 2. Sobrevive |
|
1046 (100.0%) | 0 (0.0%) | |||||||||||||||||||||||||||||||||||||||||||
| 3 | sex [factor] | 1. Hombre 2. Mujer |
|
1046 (100.0%) | 0 (0.0%) | |||||||||||||||||||||||||||||||||||||||||||
| 4 | age [numeric] | Mean (sd) : 29.9 (14.4) min < med < max: 0.2 < 28 < 80 IQR (CV) : 18 (0.5) | 98 distinct values | 1046 (100.0%) | 0 (0.0%) | |||||||||||||||||||||||||||||||||||||||||||
| 5 | sibsp [numeric] | Mean (sd) : 0.5 (0.9) min < med < max: 0 < 0 < 8 IQR (CV) : 1 (1.8) |
|
1046 (100.0%) | 0 (0.0%) | |||||||||||||||||||||||||||||||||||||||||||
| 6 | parch [numeric] | Mean (sd) : 0.4 (0.8) min < med < max: 0 < 0 < 6 IQR (CV) : 1 (2) |
|
1046 (100.0%) | 0 (0.0%) |
Generated by summarytools 0.9.9 (R version 4.0.2)
2021-06-14
Para esta práctica nos centraremos en las variables sex y survived. Como podemos notar la categoría de respuesta de estas variables posee dos niveles (1 y 2), es decir, estamos ante variables dicotómicas.
Con la función ctable del paquete summarytools podemos realizar una tabla de contingencia donde se señala la proporción de sobrevivientes según sexo
ctable(tt$sex, tt$survived)Cross-Tabulation, Row Proportions
sex * survived
Data Frame: tt| survived | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sex | No sobrevive | Sobrevive | Total | |||||||||
| Hombre | 523 | ( | 79.5% | ) | 135 | ( | 20.5% | ) | 658 | ( | 100.0% | ) |
| Mujer | 96 | ( | 24.7% | ) | 292 | ( | 75.3% | ) | 388 | ( | 100.0% | ) |
| Total | 619 | ( | 59.2% | ) | 427 | ( | 40.8% | ) | 1046 | ( | 100.0% | ) |
Generated by summarytools 0.9.9 (R version 4.0.2)
2021-06-14
La tabla muestra que la mayoría de los tripulantes no sobrevivió (619, 59,2% no sobreviven, mientras que 427, 40.8% si sobreviven). A su vez, solo un 20.5% de los hombres sobrevive, contrastando con un 75% para las mujeres.
Una forma gráfica de verlo es por medio del paquete ggmosaic que con su función geom_mosaic permite construir visualizaciones para datos categóricos. El mosaico general corresponde al total de tripulantes del titanic. Como podrán notar, hay más hombres tripulantes que mujeres, por lo que las barras para hombres son mas anchas. Luego, gracias al comando fill del geom_mosaic podemos distinguir en hombres y mujeres la proporción de cuantos sobrevivieron y cuantos no sobrevivieron.
p1 <- ggplot(data = tt) +
geom_mosaic(aes(product(survived, sex), fill= survived)) + labs(y = "Sobreviviente", x = "Sexo")
p1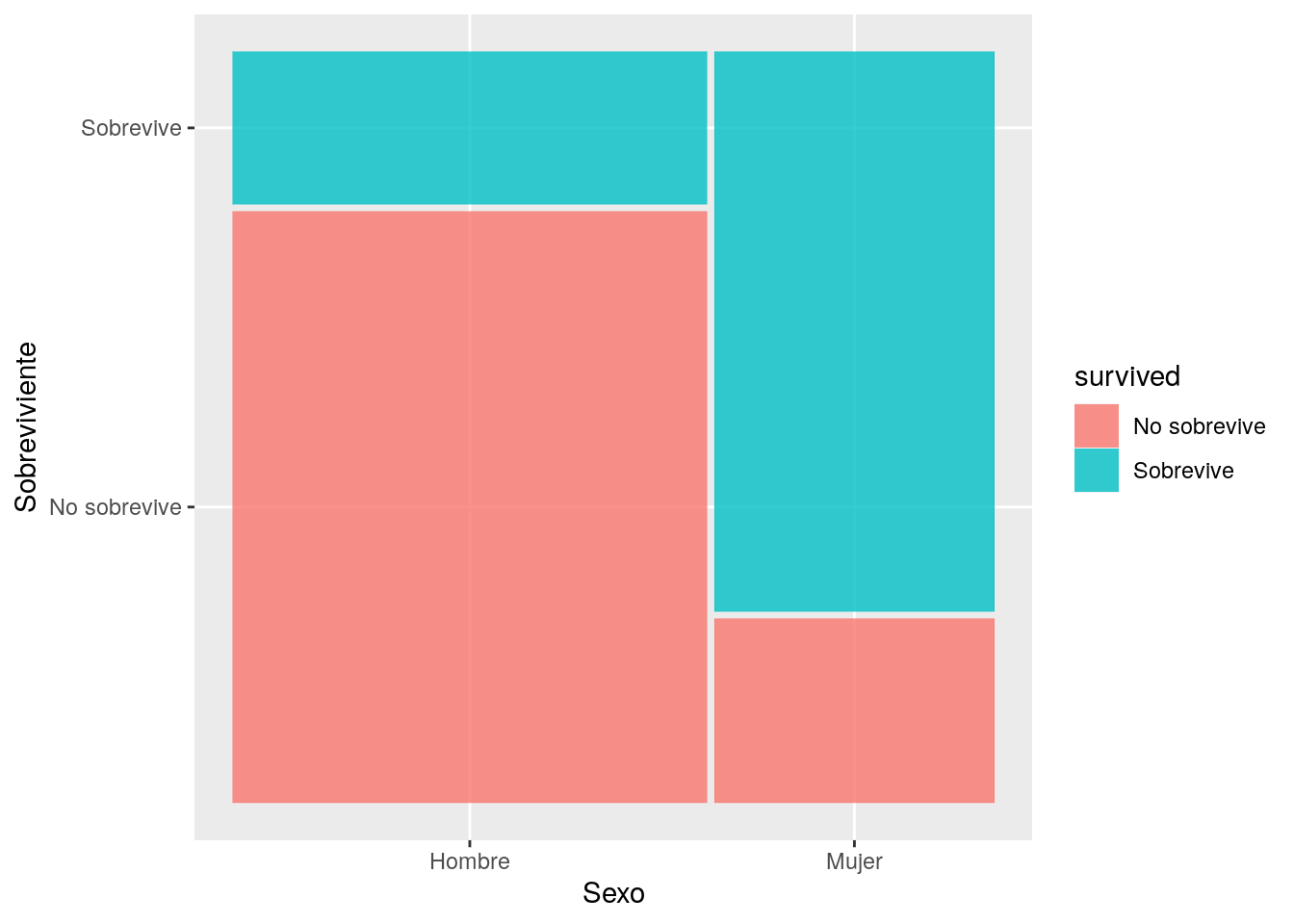
Conceptos centrales
Probabilidades
Una probabilidad es la posibilidad de ocurrencia de un evento de interés, usando como referencia todos los eventos. Por ejemplo, la probabilidad de “ser sobreviviente en el titanic” se calcula en relación a todos los tripulantes del titanic.
En primera instancia, podríamos decir que del total de pasajeros, un 40.8% de ellos sobrevive, es decir, la probabilidad de sobrevivir es de 0.408
\[Probabilidades_{sobrevivientes} = \frac{427}{1046} = 0.408\] Mientras que un 59.2% de los tripulantes no sobrevive, es decir, la probabilidad de no sobrevivir es de 0.592
\[Probabilidades_{sobrevivientes} = \frac{619}{1046} = 0.592\]
En R se realiza a través de la función prop.table
prop.table(table(tt$survived))##
## No sobrevive Sobrevive
## 0.5917782 0.4082218Odds
Una forma alternativa de representar una probabilidad son las chances o odds que se definen como la división entre el número de ocurrencias (\(\pi\)) y el numero de “no ocurrencias” (\(1-\pi\)).
\[Odd = \frac{\pi}{1-\pi}\]
Si seguimos el ejemplo del Titanic
\[Odds = \frac{Sobrevivientes}{No{Sobrevivientes}}\]
La función addmargins nos entrega las frecuencias marginales y absolutas para columnas (sexo) y filas (sobrevivencia)
addmargins(table(tt$survived,tt$sex))##
## Hombre Mujer Sum
## No sobrevive 523 96 619
## Sobrevive 135 292 427
## Sum 658 388 1046\[Odds = \frac{Sobrevivientes}{No{Sobrevivientes}}=\frac{427}{619}=0.68\]
Si hacemos el cálculo de los odds obtenemos 0.68 (427/619), es decir, hay 0.68 sobrevivientes por cada no sobreviviente. Aunque parezca poco “lógico” hablar de 0.68 sobrevivientes, esto indica que la relación entre sobrevivientes y no sobrevivientes no es 1:1 y de hecho existen más chances de morir que de sobrevivir.
Otra forma de leer este dato es decir que por cada 100 no sobrevivientes, hay 68 sobrevivientes.
Podríamos también calcular el odds de sobrevivencia de hombres y mujeres
\[Odds{hombres} = \frac{135}{523} = 0.258\] \[Odds{mujeres} = \frac{292}{96} = 3.04\]
Para los hombres, hay más chances de no sobrevivir que de sobrevivir (odds < 1), mientras que para mujeres hay más chances de sobrevivir que de no sobrevivir (odds > 1)
Propiedades de Odds
- Odds menores que 1, indican una chance negativa
- Odds mayores que 1, indican una chance positiva
En R podemos realizar este calculo directamente a través de las probabilidades marginales para cada sexo que entrega prop.table.El número 2 indica que las proporciones están calculadas por columna, es decir, las probabilidades indicadas se calculan considerando como total cada sexo.
prop.table(table(tt$survived,tt$sex),2)##
## Hombre Mujer
## No sobrevive 0.7948328 0.2474227
## Sobrevive 0.2051672 0.7525773Odds Ratio (OR)
Ahora bien, con los datos hasta ahí podriamos llegar a la conclusión de que las mujeres tienen más chances de sobrevivir que los hombres. Pero, ¿cuánto más sobreviven las mujeres que los hombres?
Esta pregunta implica la asociación entre sobrevivencia y sexo y ya no solo hablar de las chances de sobrevivencia de cada sexo por separado. Para hacer esa relación se requiere calcular los odds ratio o razón de chances.
\[Odds Ratio = \frac{Odds_{mujeres}}{Odds_{hombres}} = \frac{3.04}{0.258} = 11.78\]
El resultado que obtenemos se lee de la siguiente manera: las chances de sobrevivir de las mujeres es 11.78 veces más grande que la de los hombres.
En consecuencia, la comparación de los Odds de dos grupos es conocido como Odds Ratio (OR). Formalmente:
\[Odds_{ratio}=\frac{odds_{1}}{odds_{2}}=\frac{\pi_{1}/(1-\pi_{1})}{\pi_{2}/(1-\pi_{2})}\]
Propiedades de Odds Ratio:
Cuando X e Y son independientes \(Odds_{ratio}=1\) ya que \(odds_{1}=odds_{2}\)
El rango de posibles valores es: \(0<Odds_{ratio}<\infty\)
Cuando los valores van de 0 a 1, \(Odds_{ratio}\) indica que \(odds_{1}<odds_{2}\)
Cuando los valores van de 1 a \(\infty\), \(Odds_{ratio}\) indica que \(odds_{1}>odds_{2}\)
Es una medida de magnitud de asociación simétrica: un \(Odds_{ratio}=4\) es una asociación positiva proporcional a la asociación negativa \(Odds_{ratio}=1/4=0.25\)
¿Qué ganamos con el odds-ratio?
El OR permite expresar en un número la relación entre variables categóricas, o al menos cuando una de ellas es categórica. De esta forma, es una medida de asociación similar al sentido del \(\beta\) de regresión, y que nos permitirá aprovechar las ventajas del modelo de regresión (principalmente el control estadístico) cuando tenemos variables dependientes categóricas.
Sin embargo, los odds también poseen algunas limitaciones por resolver y que requieren su transformación para ajustarlos al modelo de regresión. Esta transformación es el logaritmo de los odds o logit (de ahí el nombre de regresión logística), tema del siguiente práctico.
Video tutorial
Reporte de progreso
Contestar aquí.