class: front <!--- Para correr en ATOM - open terminal, abrir R (simplemente, R y enter) - rmarkdown::render('static/docpres/07_interacciones/7interacciones.Rmd', 'xaringan::moon_reader') About macros.js: permite escalar las imágenes como [scale 50%](path to image), hay si que grabar ese archivo js en el directorio. ---> .pull-left[ # Estadística Multivariada ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 1er Sem 2021 ## [multivariada.netlify.com](https://multivariada.netlify.com) ] .pull-right[ .right[  <br> # Sesión 3: Regresión simple 1 ] ] ??? --- class: inverse ## Contenidos 1. Repaso de sesión anterior 2. Varianza, covarianza y correlación 3. Regresión simple 1 --- class: roja, middle, center # 1. Repaso sesión anterior --- # Base de Datos * Forma "rectangular" de almacenamiento de datos: .center[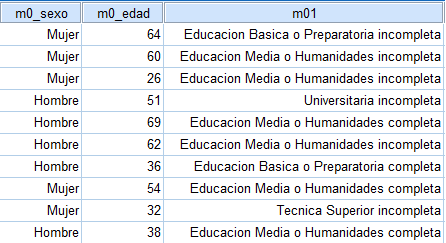] --- # Variables - Categóricas o discretas (Rango finito de valores): - Dicotómicas (1. Universidad Pública, 2. Universidad Privada) - Politómicas (1. Chile 2. Argentina 3. Perú ...) - Continuas: - Rango (teóricamente) infinito de valores (ej: Edad). --- .pull-left-narrow[ # Dispersión: ## Varianza ] .pull-right-wide[ 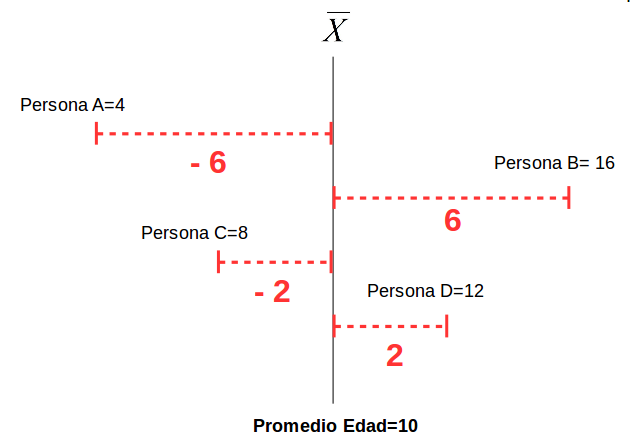 ] --- # Dispersión 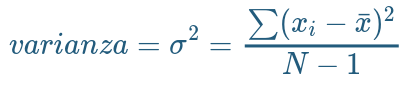 --- class: inverse, middle, center #La VARIANZA equivale al promedio de la suma de las diferencias del promedio al cuadrado --- class: roja, bottom, right # 2. Varianza, covarianza y correlación --- # Varianza & desviación estándar .pull-left[ .small[ | ID | Pje (x) | `$$x-\bar{x}$$` | `$$(x-\bar{x})^{2}$$` | |------|---------|----------|-----------| | 1 | 6 | 0.4 | 0.16 | | 2 | 4 | -1.6 | 2.56 | | 3 | 7 | 1.4 | 1.96 | | 4 | 2 | -3.6 | 12.96 | | 5 | 9 | 3.4 | 11.56 | | Sum | 28 | 0 | 29.2 | | Prom | 5.6 | | | ] ] .pull-right[ `\begin{align*} Varianza =\sigma^{2} &={\sum_{i=1}^{N}(x_{i}-\bar{x})^{2}\over {N - 1}}\\ \sigma^{2} &={(29.2)\over {5 - 1}}\\ \sigma^{2} &= 7.3 \\ Desv.est=\sigma &=\sqrt(7.3) \\ \sigma &= 2,7 \end{align*}` ] --- # Asociación: covarianza / correlación .pull-left[ _¿Se relaciona la variación de una variable, con la variación de otra variable?_ ] .pull-right[ .center[] ] --- # Asociación: covarianza / correlación (II) `\begin{align*} Covarianza = cov(x,y) &= \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {n-1}\\ \\ Correlación=r &= \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {(n-1)\sigma_x \sigma_y }\\ \\ alternativamente=r &= \frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^{2} \sum(y-\bar{y})^{2}}} \end{align*}` --- .pull-left-narrow[ .left[ ### Ejemplo de correlación `\(r= \frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^{2} \sum(y-\bar{y})^{2}}}\)` `$$=\frac{-63}{\sqrt{210*68}}$$` `$$=-0.5272$$` ] ] .pull-right-wide[ .tiny[ <br> | id| x | y | (A) `$$x-\bar{x}$$` | (B) `$$y-\bar{y}$$` | A*B | `$$(x-\bar{x})^{2}$$` | `$$(y-\bar{y})^{2}$$` | |---:|---:|---:|--------:|--------:|---------:|---------:|---------:| | 1 | 17 | 24 | -3 | 3 | -9 | 9 | 9 | | 2 | 19 | 23 | -1 | 2 | -2 | 1 | 4 | | 3 | 14 | 22 | -6 | 1 | -6 | 36 | 1 | | 4 | 22 | 17 | 2 | -4 | -8 | 4 | 16 | | 5 | 15 | 23 | -5 | 2 | -10 | 25 | 4 | | 6 | 26 | 21 | 6 | 0 | 0 | 36 | 0 | | 7 | 23 | 18 | 3 | -3 | -9 | 9 | 9 | | 8 | 21 | 17 | 1 | -4 | -4 | 1 | 16 | | 9 | 28 | 21 | 8 | 0 | 0 | 64 | 0 | | 10 | 15 | 24 | -5 | 3 | -15 | 25 | 9 | | **Sum** | | | | | -63 | 210 | 68 | | Prom | 20 | 21 | | | | | | ] ] --- # Nube de puntos (scatterplot) y correlación .center[] --- class: roja, bottom # 2. Modelo de regresión simple --- class: inverse ...sobre modelos: .orange[Del rigor de la ciencia (Borges)] .medium[En aquel Imperio, el Arte de la Cartografía logró tal Perfección que el mapa de una sola Provincia ocupaba toda una Ciudad, y el mapa del Imperio, toda una Provincia. Con el tiempo, estos Mapas Desmesurados no satisficieron y los Colegios de Cartógrafos levantaron un Mapa del Imperio, que tenía el tamaño del Imperio y coincidía puntualmente con él. Menos Adictas al Estudio de la Cartografía, las Generaciones Siguientes entendieron que ese dilatado Mapa era Inútil y no sin Impiedad lo entregaron a las Inclemencias del Sol y los Inviernos. En los desiertos del Oeste perduran despedazadas Ruinas del Mapa, habitadas por Animales y por Mendigos; en todo el País no hay otra reliquia de las Disciplinas Geográficas.] .tiny[Suárez Miranda, Viajes de Varones Prudentes, Libro Cuarto, Cap. XLV, Lérida, 1658.] --- # Objetivos centrales del modelo de regresión: 1. **Conocer**: la variación de la variable dependiente de acuerdo a la variación de otra(s) variable(s) independiente(s) 2. **Predecir**: estimar el valor de una variable (dependiente) de acuerdo al valor de otra(s) 3. **Inferir**: Establecer en que medida esta asociación es estadísticamente significativa --- # Objetivos centrales del modelo de regresión: Ejemplo 1. *Conocer*: Ej: En qué medida el puntaje PSU influye en el éxito académico en la universidad? -- 2. *Predecir*: Ej: Si una persona obtiene 600 puntos en la PSU, que promedio de notas en la universidad es probable que obtenga? (Atención: predicción no implica explicación) -- 3. *Inferir*: ¿Se puede generalizar a la población? ¿Con qué nivel de confianza? --- # Terminología variables .center[] --- # Ejemplo ### _¿En qué medida la experiencia previa jugando un juego predice el número de puntos obtenidos (en juego posterior)?_ .center[] --- .left-column[ # Datos ] .pull-left-narrow[  ] .pull-right[ .small[ ```r ggplotly(ggplot(datos, aes(x=juegos_x, y=puntos_y)) + geom_point() + expand_limits(x=c(0,6), y=c(0,7)) + coord_fixed() + scale_x_continuous(breaks = seq(min(0), max(6), by = 1)) + scale_y_continuous(breaks = seq(min(0), max(6), by = 1)) ) ``` <div id="htmlwidget-af01e3caa068ee1824b0" style="width:396px;height:396px;" class="plotly html-widget"></div> <script type="application/json" data-for="htmlwidget-af01e3caa068ee1824b0">{"x":{"data":[{"x":[0,0,1,1,1,2,2,2,2,3,3,3,3,3,4,4,4,4,5,5,5,6,6],"y":[2,3,2,3,4,2,3,4,5,2,3,4,5,6,3,4,5,6,4,5,6,5,6],"text":["juegos_x: 0<br />puntos_y: 2","juegos_x: 0<br />puntos_y: 3","juegos_x: 1<br />puntos_y: 2","juegos_x: 1<br />puntos_y: 3","juegos_x: 1<br />puntos_y: 4","juegos_x: 2<br />puntos_y: 2","juegos_x: 2<br />puntos_y: 3","juegos_x: 2<br />puntos_y: 4","juegos_x: 2<br />puntos_y: 5","juegos_x: 3<br />puntos_y: 2","juegos_x: 3<br />puntos_y: 3","juegos_x: 3<br />puntos_y: 4","juegos_x: 3<br />puntos_y: 5","juegos_x: 3<br />puntos_y: 6","juegos_x: 4<br />puntos_y: 3","juegos_x: 4<br />puntos_y: 4","juegos_x: 4<br />puntos_y: 5","juegos_x: 4<br />puntos_y: 6","juegos_x: 5<br />puntos_y: 4","juegos_x: 5<br />puntos_y: 5","juegos_x: 5<br />puntos_y: 6","juegos_x: 6<br />puntos_y: 5","juegos_x: 6<br />puntos_y: 6"],"type":"scatter","mode":"markers","marker":{"autocolorscale":false,"color":"rgba(0,0,0,1)","opacity":1,"size":5.66929133858268,"symbol":"circle","line":{"width":1.88976377952756,"color":"rgba(0,0,0,1)"}},"hoveron":"points","showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null},{"visible":false,"showlegend":false,"xaxis":"x","yaxis":"y","hoverinfo":"text","frame":null}],"layout":{"margin":{"t":23.3059360730594,"r":7.30593607305936,"b":37.2602739726027,"l":31.4155251141553},"plot_bgcolor":"rgba(235,235,235,1)","paper_bgcolor":"rgba(255,255,255,1)","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187},"xaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-0.3,6.3],"tickmode":"array","ticktext":["0","1","2","3","4","5","6"],"tickvals":[0,1,2,3,4,5,6],"categoryorder":"array","categoryarray":["0","1","2","3","4","5","6"],"nticks":null,"ticks":"outside","tickcolor":"rgba(51,51,51,1)","ticklen":3.65296803652968,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(77,77,77,1)","family":"","size":11.689497716895},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(255,255,255,1)","gridwidth":0.66417600664176,"zeroline":false,"anchor":"y","title":{"text":"juegos_x","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187}},"scaleanchor":"y","scaleratio":1,"hoverformat":".2f"},"yaxis":{"domain":[0,1],"automargin":true,"type":"linear","autorange":false,"range":[-0.35,7.35],"tickmode":"array","ticktext":["0","1","2","3","4","5","6"],"tickvals":[0,1,2,3,4,5,6],"categoryorder":"array","categoryarray":["0","1","2","3","4","5","6"],"nticks":null,"ticks":"outside","tickcolor":"rgba(51,51,51,1)","ticklen":3.65296803652968,"tickwidth":0.66417600664176,"showticklabels":true,"tickfont":{"color":"rgba(77,77,77,1)","family":"","size":11.689497716895},"tickangle":-0,"showline":false,"linecolor":null,"linewidth":0,"showgrid":true,"gridcolor":"rgba(255,255,255,1)","gridwidth":0.66417600664176,"zeroline":false,"anchor":"x","title":{"text":"puntos_y","font":{"color":"rgba(0,0,0,1)","family":"","size":14.6118721461187}},"scaleanchor":"x","scaleratio":1,"hoverformat":".2f"},"shapes":[{"type":"rect","fillcolor":null,"line":{"color":null,"width":0,"linetype":[]},"yref":"paper","xref":"paper","x0":0,"x1":1,"y0":0,"y1":1}],"showlegend":false,"legend":{"bgcolor":"rgba(255,255,255,1)","bordercolor":"transparent","borderwidth":1.88976377952756,"font":{"color":"rgba(0,0,0,1)","family":"","size":11.689497716895}},"hovermode":"closest","barmode":"relative"},"config":{"doubleClick":"reset","showSendToCloud":false},"source":"A","attrs":{"573b241d4d84":{"x":{},"y":{},"type":"scatter"},"573b501c86ba":{"x":{},"y":{}}},"cur_data":"573b241d4d84","visdat":{"573b241d4d84":["function (y) ","x"],"573b501c86ba":["function (y) ","x"]},"highlight":{"on":"plotly_click","persistent":false,"dynamic":false,"selectize":false,"opacityDim":0.2,"selected":{"opacity":1},"debounce":0},"shinyEvents":["plotly_hover","plotly_click","plotly_selected","plotly_relayout","plotly_brushed","plotly_brushing","plotly_clickannotation","plotly_doubleclick","plotly_deselect","plotly_afterplot","plotly_sunburstclick"],"base_url":"https://plot.ly"},"evals":[],"jsHooks":[]}</script> ] ] --- # Descriptivos ```r stargazer(datos, type = "html") ``` <table style="text-align:center"><tr><td colspan="8" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Statistic</td><td>N</td><td>Mean</td><td>St. Dev.</td><td>Min</td><td>Pctl(25)</td><td>Pctl(75)</td><td>Max</td></tr> <tr><td colspan="8" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">id</td><td>23</td><td>12.000</td><td>6.782</td><td>1</td><td>6.5</td><td>17.5</td><td>23</td></tr> <tr><td style="text-align:left">juegos_x</td><td>23</td><td>3.000</td><td>1.758</td><td>0</td><td>2</td><td>4</td><td>6</td></tr> <tr><td style="text-align:left">puntos_y</td><td>23</td><td>4.000</td><td>1.382</td><td>2</td><td>3</td><td>5</td><td>6</td></tr> <tr><td colspan="8" style="border-bottom: 1px solid black"></td></tr></table> --- .left-column[ # **Medias condicionales** ] .center[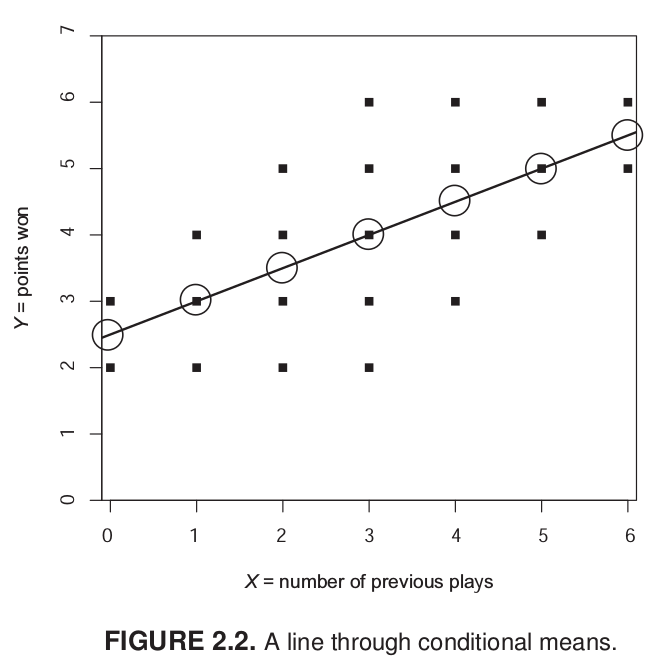] ??? Ejemplo para los sujetos con 1 en X hay 3 valores de Y: 2, 3 y 4. Por lo tanto, la media condicional de Y dado X=1 es 3 --- .left-column[ # Idea de distribución condicional ] .center[] --- .left-column[ # La recta de regresión ] .right-column[ .center[] .small[ La (co) variación general de Y respecto a X se puede expresar en una ecuación de la recta = **modelo de regresión** ] ] --- class: inverse, right ## Para obtener la “mejor recta” se utiliza la estimación de mínimos cuadrados (EMC, o **OLS** – Ordinary Least Squares) -- ## OLS minimiza la suma de los **residuos** = distancias entre las observaciones y la recta en el eje vertical --- # Componentes de la ecuación de la recta de regresión `$$\widehat{Y}=b_{0} +b_{1}X$$` Donde - `\(\widehat{Y}\)` es el valor estimado de `\(Y\)` - `\(b_{0}\)` es el intercepto de la recta (el valor de Y cuando X es 0) - `\(b_{1}\)` es el coeficiente de regresión, que nos dice cuánto aumenta Y por cada punto que aumenta X --- # Estimación de los coeficientes de la ecuación: `$$b_{1}=\frac{Cov(XY)}{VarX}$$` `$$b_{1}=\frac{\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {n-1}}{\frac{\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})} {n-1}}$$` Y simplificando `$$b_{1}=\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})}$$` --- # Estimación de los coeficientes de la ecuación: Luego despejando el valor de `\(b_{0}\)` `$$b_{0}=\bar{Y}-b_{1}\bar{X}$$` --- # Cálculo de coeficientes La base para todos estos calculos es la diferencia de cada valor menos su promedio. Para ello: 1. Vamos a crear los siguientes vectores (variables) en nuestra base de datos `$$difx=x-\bar{x}$$` `$$dify=y-\bar{y}$$` --- # Cálculo basado en el ejemplo 2.Con la información anterior podemos obtener la diferencia de productos cruzados `$$difcru=(x-\bar{x})*(y-\bar{y})$$` 3.También obtenemos las diferencias del promedio al cuadrado de X= `$$difx2=(x-\bar{x})^2$$` --- class: split-40 count: false .column[.content[ ```r *datos_b <-datos datos_b ``` ]] .column[.content[ ``` ## id juegos_x puntos_y ## 1 1 0 2 ## 2 2 0 3 ## 3 3 1 2 ## 4 4 1 3 ## 5 5 1 4 ## 6 6 2 2 ## 7 7 2 3 ## 8 8 2 4 ## 9 9 2 5 ## 10 10 3 2 ## 11 11 3 3 ## 12 12 3 4 ## 13 13 3 5 ## 14 14 3 6 ## 15 15 4 3 ## 16 16 4 4 ## 17 17 4 5 ## 18 18 4 6 ## 19 19 5 4 ## 20 20 5 5 ## 21 21 5 6 ## 22 22 6 5 ## 23 23 6 6 ``` ]] --- class: split-40 count: false .column[.content[ ```r datos_b <-datos *datos$p_x <- mean(datos$juegos_x) datos_b ``` ]] .column[.content[ ``` ## id juegos_x puntos_y ## 1 1 0 2 ## 2 2 0 3 ## 3 3 1 2 ## 4 4 1 3 ## 5 5 1 4 ## 6 6 2 2 ## 7 7 2 3 ## 8 8 2 4 ## 9 9 2 5 ## 10 10 3 2 ## 11 11 3 3 ## 12 12 3 4 ## 13 13 3 5 ## 14 14 3 6 ## 15 15 4 3 ## 16 16 4 4 ## 17 17 4 5 ## 18 18 4 6 ## 19 19 5 4 ## 20 20 5 5 ## 21 21 5 6 ## 22 22 6 5 ## 23 23 6 6 ``` ]] --- class: split-40 count: false .column[.content[ ```r datos_b <-datos datos$p_x <- mean(datos$juegos_x) *datos$difx <-datos$juegos_x-datos$p_x datos_b ``` ]] .column[.content[ ``` ## id juegos_x puntos_y p_x ## 1 1 0 2 3 ## 2 2 0 3 3 ## 3 3 1 2 3 ## 4 4 1 3 3 ## 5 5 1 4 3 ## 6 6 2 2 3 ## 7 7 2 3 3 ## 8 8 2 4 3 ## 9 9 2 5 3 ## 10 10 3 2 3 ## 11 11 3 3 3 ## 12 12 3 4 3 ## 13 13 3 5 3 ## 14 14 3 6 3 ## 15 15 4 3 3 ## 16 16 4 4 3 ## 17 17 4 5 3 ## 18 18 4 6 3 ## 19 19 5 4 3 ## 20 20 5 5 3 ## 21 21 5 6 3 ## 22 22 6 5 3 ## 23 23 6 6 3 ``` ]] --- class: split-40 count: false .column[.content[ ```r datos_b <-datos datos$p_x <- mean(datos$juegos_x) datos$difx <-datos$juegos_x-datos$p_x *datos$p_y <- mean(datos$puntos_y) datos_b ``` ]] .column[.content[ ``` ## id juegos_x puntos_y p_x difx ## 1 1 0 2 3 -3 ## 2 2 0 3 3 -3 ## 3 3 1 2 3 -2 ## 4 4 1 3 3 -2 ## 5 5 1 4 3 -2 ## 6 6 2 2 3 -1 ## 7 7 2 3 3 -1 ## 8 8 2 4 3 -1 ## 9 9 2 5 3 -1 ## 10 10 3 2 3 0 ## 11 11 3 3 3 0 ## 12 12 3 4 3 0 ## 13 13 3 5 3 0 ## 14 14 3 6 3 0 ## 15 15 4 3 3 1 ## 16 16 4 4 3 1 ## 17 17 4 5 3 1 ## 18 18 4 6 3 1 ## 19 19 5 4 3 2 ## 20 20 5 5 3 2 ## 21 21 5 6 3 2 ## 22 22 6 5 3 3 ## 23 23 6 6 3 3 ``` ]] --- class: split-40 count: false .column[.content[ ```r datos_b <-datos datos$p_x <- mean(datos$juegos_x) datos$difx <-datos$juegos_x-datos$p_x datos$p_y <- mean(datos$puntos_y) *datos$dify <-datos$puntos_y-datos$p_y datos_b ``` ]] .column[.content[ ``` ## id juegos_x puntos_y p_x difx p_y ## 1 1 0 2 3 -3 4 ## 2 2 0 3 3 -3 4 ## 3 3 1 2 3 -2 4 ## 4 4 1 3 3 -2 4 ## 5 5 1 4 3 -2 4 ## 6 6 2 2 3 -1 4 ## 7 7 2 3 3 -1 4 ## 8 8 2 4 3 -1 4 ## 9 9 2 5 3 -1 4 ## 10 10 3 2 3 0 4 ## 11 11 3 3 3 0 4 ## 12 12 3 4 3 0 4 ## 13 13 3 5 3 0 4 ## 14 14 3 6 3 0 4 ## 15 15 4 3 3 1 4 ## 16 16 4 4 3 1 4 ## 17 17 4 5 3 1 4 ## 18 18 4 6 3 1 4 ## 19 19 5 4 3 2 4 ## 20 20 5 5 3 2 4 ## 21 21 5 6 3 2 4 ## 22 22 6 5 3 3 4 ## 23 23 6 6 3 3 4 ``` ]] --- class: split-40 count: false .column[.content[ ```r datos_b <-datos datos$p_x <- mean(datos$juegos_x) datos$difx <-datos$juegos_x-datos$p_x datos$p_y <- mean(datos$puntos_y) datos$dify <-datos$puntos_y-datos$p_y *datos$dif_cru <-datos$difx*datos$dify datos_b ``` ]] .column[.content[ ``` ## id juegos_x puntos_y p_x difx p_y dify ## 1 1 0 2 3 -3 4 -2 ## 2 2 0 3 3 -3 4 -1 ## 3 3 1 2 3 -2 4 -2 ## 4 4 1 3 3 -2 4 -1 ## 5 5 1 4 3 -2 4 0 ## 6 6 2 2 3 -1 4 -2 ## 7 7 2 3 3 -1 4 -1 ## 8 8 2 4 3 -1 4 0 ## 9 9 2 5 3 -1 4 1 ## 10 10 3 2 3 0 4 -2 ## 11 11 3 3 3 0 4 -1 ## 12 12 3 4 3 0 4 0 ## 13 13 3 5 3 0 4 1 ## 14 14 3 6 3 0 4 2 ## 15 15 4 3 3 1 4 -1 ## 16 16 4 4 3 1 4 0 ## 17 17 4 5 3 1 4 1 ## 18 18 4 6 3 1 4 2 ## 19 19 5 4 3 2 4 0 ## 20 20 5 5 3 2 4 1 ## 21 21 5 6 3 2 4 2 ## 22 22 6 5 3 3 4 1 ## 23 23 6 6 3 3 4 2 ``` ]] --- class: split-40 count: false .column[.content[ ```r datos_b <-datos datos$p_x <- mean(datos$juegos_x) datos$difx <-datos$juegos_x-datos$p_x datos$p_y <- mean(datos$puntos_y) datos$dify <-datos$puntos_y-datos$p_y datos$dif_cru <-datos$difx*datos$dify *datos$difx2 <-datos$difx^2 datos_b ``` ]] .column[.content[ ``` ## id juegos_x puntos_y p_x difx p_y dify dif_cru ## 1 1 0 2 3 -3 4 -2 6 ## 2 2 0 3 3 -3 4 -1 3 ## 3 3 1 2 3 -2 4 -2 4 ## 4 4 1 3 3 -2 4 -1 2 ## 5 5 1 4 3 -2 4 0 0 ## 6 6 2 2 3 -1 4 -2 2 ## 7 7 2 3 3 -1 4 -1 1 ## 8 8 2 4 3 -1 4 0 0 ## 9 9 2 5 3 -1 4 1 -1 ## 10 10 3 2 3 0 4 -2 0 ## 11 11 3 3 3 0 4 -1 0 ## 12 12 3 4 3 0 4 0 0 ## 13 13 3 5 3 0 4 1 0 ## 14 14 3 6 3 0 4 2 0 ## 15 15 4 3 3 1 4 -1 -1 ## 16 16 4 4 3 1 4 0 0 ## 17 17 4 5 3 1 4 1 1 ## 18 18 4 6 3 1 4 2 2 ## 19 19 5 4 3 2 4 0 0 ## 20 20 5 5 3 2 4 1 2 ## 21 21 5 6 3 2 4 2 4 ## 22 22 6 5 3 3 4 1 3 ## 23 23 6 6 3 3 4 2 6 ``` ]] --- class: split-40 count: false .column[.content[ ```r datos_b <-datos datos$p_x <- mean(datos$juegos_x) datos$difx <-datos$juegos_x-datos$p_x datos$p_y <- mean(datos$puntos_y) datos$dify <-datos$puntos_y-datos$p_y datos$dif_cru <-datos$difx*datos$dify datos$difx2 <-datos$difx^2 *datos$difx2 <-datos$difx^2 datos_b ``` ]] .column[.content[ ``` ## id juegos_x puntos_y p_x difx p_y dify dif_cru difx2 ## 1 1 0 2 3 -3 4 -2 6 9 ## 2 2 0 3 3 -3 4 -1 3 9 ## 3 3 1 2 3 -2 4 -2 4 4 ## 4 4 1 3 3 -2 4 -1 2 4 ## 5 5 1 4 3 -2 4 0 0 4 ## 6 6 2 2 3 -1 4 -2 2 1 ## 7 7 2 3 3 -1 4 -1 1 1 ## 8 8 2 4 3 -1 4 0 0 1 ## 9 9 2 5 3 -1 4 1 -1 1 ## 10 10 3 2 3 0 4 -2 0 0 ## 11 11 3 3 3 0 4 -1 0 0 ## 12 12 3 4 3 0 4 0 0 0 ## 13 13 3 5 3 0 4 1 0 0 ## 14 14 3 6 3 0 4 2 0 0 ## 15 15 4 3 3 1 4 -1 -1 1 ## 16 16 4 4 3 1 4 0 0 1 ## 17 17 4 5 3 1 4 1 1 1 ## 18 18 4 6 3 1 4 2 2 1 ## 19 19 5 4 3 2 4 0 0 4 ## 20 20 5 5 3 2 4 1 2 4 ## 21 21 5 6 3 2 4 2 4 4 ## 22 22 6 5 3 3 4 1 3 9 ## 23 23 6 6 3 3 4 2 6 9 ``` ]] --- # Cálculo basado en el ejemplo Y con esto podemos obtener la suma de productos cruzados y la suma de cuadrados de X ```r sum(datos$dif_cru) ``` ``` ## [1] 34 ``` ```r sum(datos$difx2) ``` ``` ## [1] 68 ``` --- # Reemplazando en la fórmula `$$b_{1}=\frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {\sum_{i=1}^{n}(x_i - \bar{x})(x_i - \bar{x})}=\frac{34}{68}=0.5$$` --- # Cálculo basado en el ejemplo Reemplazando podemos obtener el valor de `\(b_{0}\)` `$$b_{0}=\bar{Y}-b_{1}\bar{X}$$` `$$b_{0}=4-(3 * 0.5)=2.5$$` Completando la ecuación: `$$\widehat{Y}=2.5+0.5X$$` Por cada unidad que aumenta la experiencia en juego (x), los puntos obtenidos(y) aumentan en 0.5. --- # Cálculo basado en el ejemplo `$$\widehat{Y}=2.5+0.5X$$` Esto nos permite estimar el valor de `\(Y\)` (o su media condicional) basado en el puntaje `\(X\)`. Por ejemplo, cuál es el valor estimado de `\(Y\)` dado `\(X=3\)`? `$$\widehat{Y}=2.5+(0.5*3)$$` `$$\widehat{Y}=2.5+(3*0.5)=4$$` El valor estimado de puntos para una persona que ha jugado 3 veces es 4. --- .left-column[ ## Cálculo basado en el ejemplo ] .small[ .center[ ```r ggplot(datos, aes(x=juegos_x, y=puntos_y)) + geom_point() + geom_smooth(method=lm, se=FALSE) ``` <!-- --> ] ] --- # En resumen: ¿qué gano con el modelo de regresión? Al igual que en correlación - intensidad de la relación entre variables - dirección de la relación Y además: - predicción en el puntaje real de la variable dependiente - estimación del ajuste o cantidad de error en la estimación (próxima clase) - incluir más de una variable predictora (en 2 clases más) --- class: inverse, middle, center # Regresión simple en R --- # Estimación del modelo de regresión simple en `R` La función para estimar regresión en `R` es `lm` (linear model): .small[ ``` objeto=lm(dependiente ~ independiente, data=datos) ```] Donde - *objeto*: el nombre (cualquiera) que le damos al objeto donde se guardan los resultados de la estimación - *dependiente / independiente*: los nombres de las variables en los datos - *datos* = el nombre del objeto de nuestros datos en R --- # Estimación del modelo de regresión simple en `R` En nuestro ejemplo: ```r reg1 <-lm(puntos_y ~ juegos_x, data = datos) ``` `reg1` es el objeto que almacena la información de nuestra estimación. Para un reporte simple: ```r reg1 ``` --- ```r reg1 ``` ``` ## ## Call: ## lm(formula = puntos_y ~ juegos_x, data = datos) ## ## Coefficients: ## (Intercept) juegos_x ## 2.5 0.5 ``` --- # Y en formato publicable <br> <table style="border-collapse:collapse; border:none;"> <tr> <th style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; text-align:left; "> </th> <th colspan="2" style="border-top: double; text-align:center; font-style:normal; font-weight:bold; padding:0.2cm; ">Modelo 1</th> </tr> <tr> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; text-align:left; ">Predictores</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">β</td> <td style=" text-align:center; border-bottom:1px solid; font-style:italic; font-weight:normal; ">p</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">(Intercept)</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">2.500</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "><strong><0.001</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; ">juegos_x</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; ">0.500</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:center; "><strong>0.001</strong></td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm; border-top:1px solid;">Observations</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left; border-top:1px solid;" colspan="2">23</td> </tr> <tr> <td style=" padding:0.2cm; text-align:left; vertical-align:top; text-align:left; padding-top:0.1cm; padding-bottom:0.1cm;">R<sup>2</sup> / R<sup>2</sup> adjusted</td> <td style=" padding:0.2cm; text-align:left; vertical-align:top; padding-top:0.1cm; padding-bottom:0.1cm; text-align:left;" colspan="2">0.405 / 0.376</td> </tr> </table> --- class: roja, right # Próxima semana: ## - Ajuste ## - Residuos ## - Lectura: [Moore: 2. Análisis de relaciones](../../docs/lecturas/moore_analisisderelaciones1.pdf) --- class: front .pull-left[ # Estadística Multivariada ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 1er Sem 2021 ## [multivariada.netlify.com](https://multivariada.netlify.com) ] .pull-right[ .right[ <br>  ] ]